Matututo ka:
Ang mga integral kasama ang mga derivative ay ang mga pangunahing bagay sa calculus. Ang proseso ng pag-compute ng isang integral ay tinatawag na integration at ang approximate computation ng isang integral ay tinatawag bilang numerical integration.
Mayroong dalawang klase ng integral - definite integral (tulad ng 5) at Indefinite integral, na may mas mababa at itaas na limitasyon tulad ng \(\int_a^bf(x) \cdot dx\) .
Ano ang Integral?
Sabihin nating kailangan nating hanapin ang lugar sa ilalim ng curve at ang x-axis sa itaas.
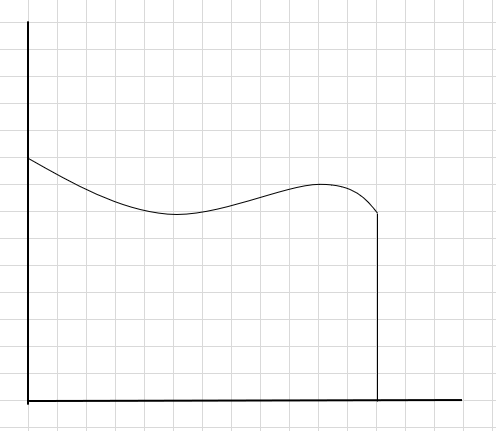
Ang isang paraan upang gawin ay ang hatiin ang rehiyon sa apat na mga segment at pagkatapos ay gumuhit ng isang parihaba (gamit ang linya ng segment na ito) upang ang kanang itaas na sulok ng bawat parihaba ay humipo sa kurba (tulad ng ibinigay sa ibaba)
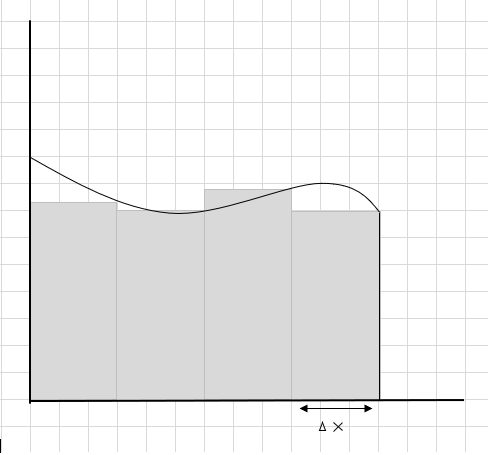
Ang kabuuan ng lugar ng mga rectangular na segment na ito ay ang tinantyang lugar sa ilalim ng curve na ito. \(\Delta x \) ang lapad ng mga parihaba/hiwa. Ano sa palagay mo ang tinatayang lugar?
Maraming bahagi ng kurba ang hindi nakuha at ang ilang karagdagang bahagi ay isinasaalang-alang habang kinakalkula ang lugar ng rehiyon ng kurba na ito. Ang pag-check-in sa ibaba ng larawan sa madilim na kulay-abo na rehiyon ay kumakatawan sa mga miss out at karagdagang mga bahagi.
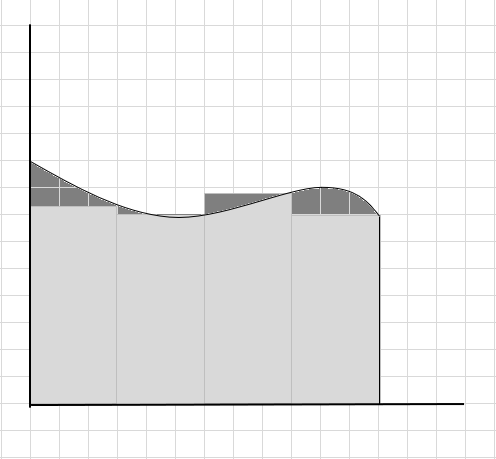
Masasabi nating ito ay isang mahinang pagtatantya ng lugar ng curved region dahil ang mga parihaba ay hindi eksaktong magkasya sa ilalim ng curve. Hatiin natin ang lugar sa ilalim ng curve na ito sa mas maliliit na segment.
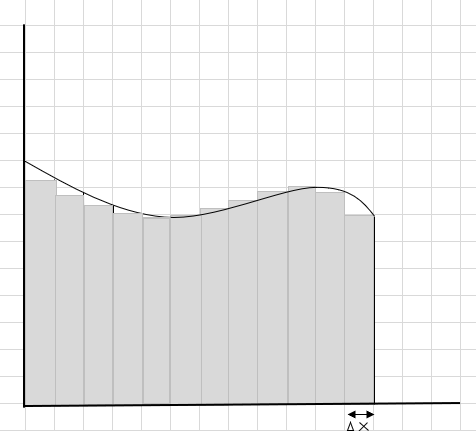
Maaari mong makita na ang mga parihaba na ito ay magkasya sa loob ng kurbadong lugar kaysa sa mas malalaking parihaba na mga segment. Subukan nating hatiin ang curved na rehiyon na ito sa mas maliliit na segment/hiwa at subukang tukuyin ang lugar sa ilalim ng curve.
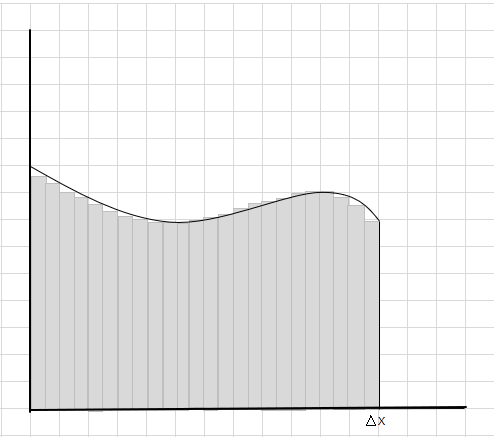
Ang mga kulang at mga karagdagang bahagi ay unti-unting nababawasan at ang mga parihaba ay mas angkop sa loob ng curve na rehiyon. Maaari naming ipahiwatig na ang kabuuan ng lugar ng lahat ng mga parihaba na ito ay nagbibigay ng isang mahusay na pagtatantya ng lugar sa ilalim ng curve. O sa madaling salita, masasabi natin habang ang mga hiwa ay lumalapit sa zero sa lapad ang sagot ay lumalapit sa totoong sagot. Sinusulat namin ngayon ang dx para sa \(\Delta x\) na nangangahulugan na ang lapad ay papalapit na sa zero.
Kunin natin ang formula para sa integral calculus dito:
Sabihin nating kailangan nating hanapin ang lugar sa ilalim ng curve na ito sa pagitan ng point a at b: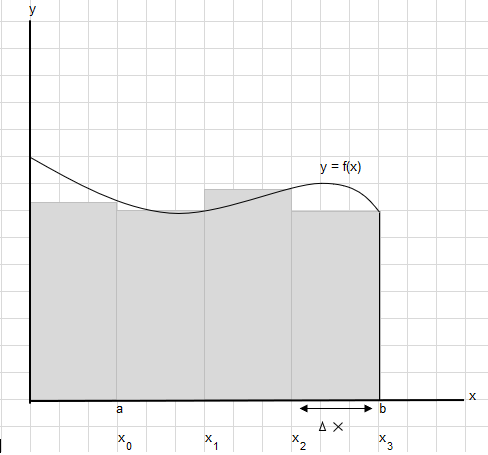
Hatiin ang lugar sa pagitan ng a at b sa pantay na mga segment upang ang lapad ng bawat parihaba ay \(\Delta x\) .
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
Ang kabuuan ng lugar ng mga parihaba na ito ay maaaring isulat bilang \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) .
Maaari tayong magkaroon ng mas mahusay na pagtatantya ng lugar habang \(\Delta x \) ay lumiliit o sa madaling salita kapag dumarami ang bilang ng mga segment. Kaya't ang \(\Delta x \) ay payat at payat at n ay palaki ng palaki. Ang ideyang ito ng pagkuha ng mas mahusay na approximation habang kinukuha natin ang limitasyon habang ang n ay lumalapit sa infinity at ang \(\Delta x \) ay nagiging infinitesimal na maliit ay Integral.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) ay kumakatawan sa lugar sa ilalim ng f ng x sa pagitan ng x = a at x = b
Ang paghahanap ng Integral ay isang reverse ng paghahanap ng Derivatives.
Ang derivative ng x 2 ay 2x. Kaya ang isang integral ng 2x ay x 2 .
\(\int 2x \space dx = x^2 + C\) , kung saan ang C ay pare-pareho. Dahil ang derivative ng constant ay 0 kaya ang derivative ng x 2 , x 2 +4, x 2 +10, x 2 +99 ay 2x. Samakatuwid ang integral ng 2x ay x 2 +C.
Tingnan natin ang mga integral ng mga karaniwang function:
| Mga Karaniwang Pag-andar | Function | integral |
| pare-pareho | \(\int a \cdot dx\) | \(ax + c\) |
| Variable | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Square | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| Exponential | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Trigonometry(x sa radians) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Mga Karaniwang Panuntunan sa Pagsasama:
| Mga tuntunin | Function | integral |
| Multiplikasyon sa pamamagitan ng pare-pareho | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Power Rule(n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Sum na Panuntunan | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Panuntunan ng Pagkakaiba | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Mga Klase ng Integrals
\(\int f(x) \space dx\) ay kumakatawan sa hindi tiyak na integral at \(\int_a^bf(x) \cdot dx\) ay kumakatawan sa isang tiyak na integral. Ang isang tiyak na integral ay may mga halaga ng simula at pagtatapos. Dito ang a at b ay tinatawag na mga limitasyon o hangganan. Ang hindi tiyak na integral ay higit pa sa isang pangkalahatang anyo ng pagsasama at maaaring bigyang-kahulugan bilang anti-derivative ng function.
Nahanap natin ang Definite Integral sa pamamagitan ng pagkalkula ng indefinite Integral sa a , at sa b , pagkatapos ay pagbabawas. Intindihin natin ito sa pamamagitan ng isang halimbawa:
Alam natin \(\int 2x \cdot dx = x^2 + C\) . Ano ang magiging halaga ng isang tiyak na integral \(\int _1^2 2x \cdot dx \) ?
Sa x =1, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
Sa x = 2, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
Ibawas (4 + C) - (1 + C) = 3
Halaga ng \(\int _1^2 2x \cdot dx \) = 3