Öğreneceksiniz:
İntegraller , türevlerle birlikte analizdeki temel nesnelerdir. Bir integrali hesaplama işlemine entegrasyon denir ve bir integralin yaklaşık olarak hesaplanmasına sayısal entegrasyon denir.
İki tür integral vardır - belirli integral (5 gibi) ve \(\int_a^bf(x) \cdot dx\) gibi alt ve üst sınırları olan belirsiz integraller.
İntegral nedir?
Diyelim ki eğrinin altındaki alanı ve yukarıdaki x eksenini bulmamız gerekiyor.
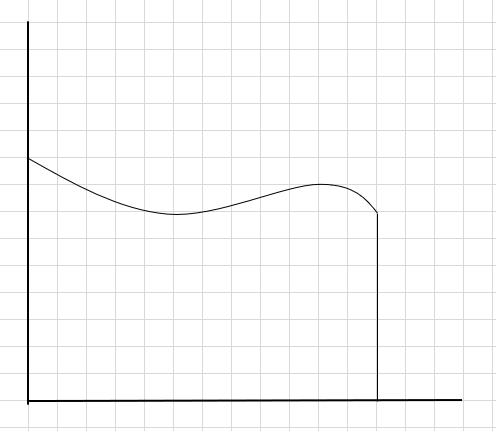
Bunu yapmanın bir yolu, bölgeyi dört parçaya bölmek ve ardından (bu parça çizgisini kullanarak) her dikdörtgenin sağ üst köşesi eğriye değecek şekilde (aşağıda verildiği gibi) bir dikdörtgen çizmektir.
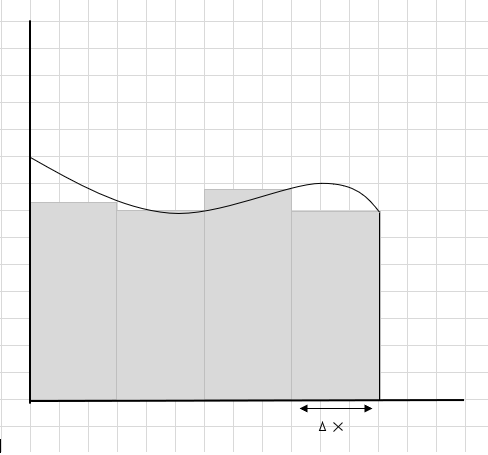
Bu dikdörtgen bölümlerin alanlarının toplamı, bu eğrinin altındaki tahmini alandır. \(\Delta x \) , dikdörtgenlerin/dilimlerin genişliğidir. Tahmini alan hakkında ne düşünüyorsunuz?
Bu eğri bölgesinin alanı hesaplanırken birçok eğri parçası atlanır ve birkaç ek parça dikkate alınır. Resmin altındaki check-in koyu gri bölge, kaçırılan ve ek parçaları temsil eder.
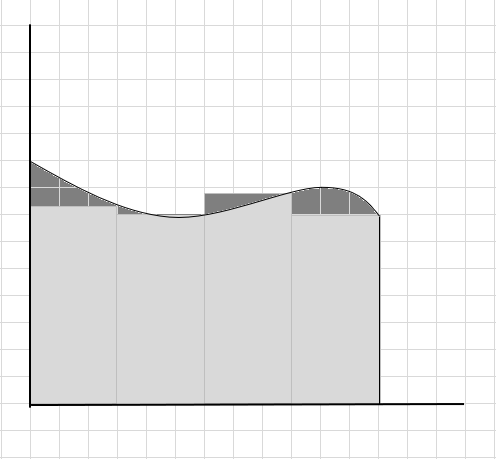
Dikdörtgenler tam olarak eğrinin altına sığmadığından, bunun eğri bölgenin alanı için zayıf bir tahmin olduğunu söyleyebiliriz. Bu eğrinin altındaki alanı daha küçük parçalara ayıralım.
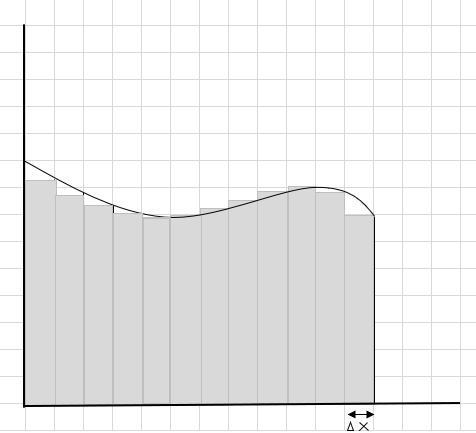
Bu dikdörtgenlerin kavisli alana daha büyük dikdörtgen parçalardan daha iyi sığdığını görebilirsiniz. Bu eğri bölgeyi daha küçük parçalara/dilimlere ayırmaya çalışalım ve eğrinin altında kalan alanı belirlemeye çalışalım.
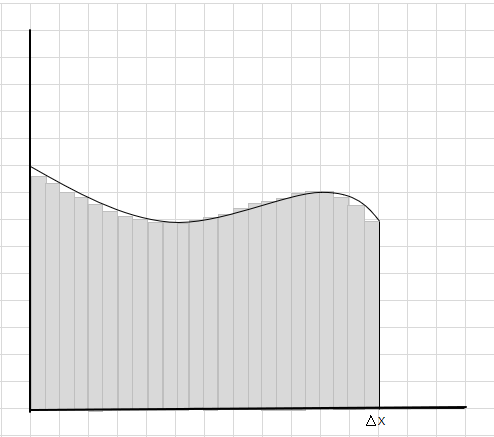
Eksik ve fazla kısımlar kademeli olarak azalıyor ve dikdörtgenler eğri bölgesinin içine çok daha iyi oturuyor. Tüm bu dikdörtgenlerin alanlarının toplamının, eğrinin altındaki alanın iyi bir tahminini verdiğini çıkarabiliriz. Ya da başka bir deyişle, dilimler sıfıra yaklaştıkça cevap doğru cevaba yaklaşır diyebiliriz. Şimdi genişliğin sıfıra yaklaştığı anlamına gelen \(\Delta x\) için dx yazıyoruz.
İntegral hesabının formülünü buradan türetelim:
Diyelim ki a ve b noktaları arasındaki bu eğrinin altındaki alanı bulmamız gerekiyor: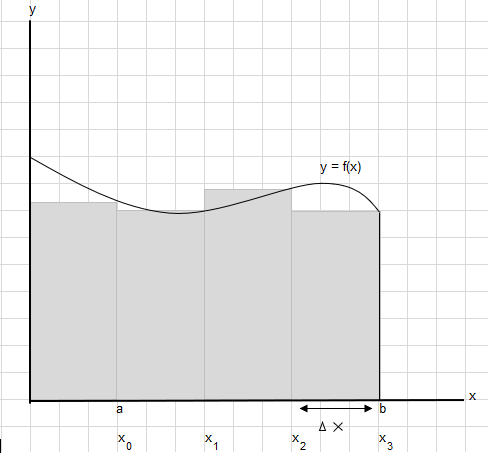
a ve b arasındaki alanı, her bir dikdörtgenin genişliği \(\Delta x\) olacak şekilde eşit parçalara bölün.
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
Bu dikdörtgenlerin alanlarının toplamı \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) olarak yazılabilir.
\(\Delta x \) küçüldükçe veya başka bir deyişle parça sayısı arttıkça alan için daha iyi bir yaklaşım elde edebiliriz. Böylece \(\Delta x \) gittikçe incelir ve n giderek büyür. n sonsuza yaklaşırken ve \(\Delta x \) sonsuz küçük hale geldikçe limiti aldığımızda daha iyi bir yaklaşım elde etme kavramı İntegral'dir.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) = \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) , x = a ile x = b arasındaki f x'in altındaki alanı temsil eder
İntegral bulma, Türev bulmanın tersidir.
x 2'nin türevi 2x'tir. Yani 2x'in bir integrali x 2'dir .
\(\int 2x \space dx = x^2 + C\) , burada C bir sabittir. Sabitin türevi 0 olduğundan x 2 , x 2 +4, x 2 +10, x 2 +99'un türevi 2x'tir. Bu nedenle 2x'in integrali x 2 +C'dir.
Ortak fonksiyonların integrallerine bakalım:
| Ortak İşlevler | İşlev | ayrılmaz |
| Devamlı | \(\int a \cdot dx\) | \(ax + c\) |
| Değişken | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Meydan | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| üstel | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Trigonometri(radyan cinsinden x) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Ortak Entegrasyon Kuralları:
| Tüzük | İşlev | ayrılmaz |
| sabit ile çarpma | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Güç Kuralı(n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Toplam Kuralı | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Fark Kuralı | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
İntegral Sınıfları
\(\int f(x) \space dx\) belirsiz integrali ve \(\int_a^bf(x) \cdot dx\) belirli bir integrali temsil eder. Belirli bir integralin başlangıç ve bitiş değerleri vardır. Burada a ve b'ye sınırlar veya sınırlar denir. Belirsiz integral, daha çok genel bir entegrasyon biçimidir ve fonksiyonun anti-türevi olarak yorumlanabilir.
Belirli İntegrali a ve b'deki belirsiz İntegrali hesaplayarak ve sonra çıkararak buluruz. Bunu bir örnekle anlayalım:
\(\int 2x \cdot dx = x^2 + C\) biliyoruz. Belirli bir \(\int _1^2 2x \cdot dx \) integralinin değeri ne olur?
x =1'de, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
x = 2'de, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
Çıkarma (4 + C) - (1 + C) = 3
\(\int _1^2 2x \cdot dx \) = 3'ün değeri