Ти навчишся:
Інтеграли разом із похідними є фундаментальними об’єктами в численні. Процес обчислення інтеграла називається інтегруванням , а наближене обчислення інтеграла — чисельним інтегруванням.
Існує два класи інтегралів — визначений інтеграл (наприклад, 5) і невизначений інтеграл, який має нижню та верхню межі, наприклад \(\int_a^bf(x) \cdot dx\) .
Що таке Інтеграл?
Припустимо, ми повинні знайти площу під кривою та віссю абсцисс.
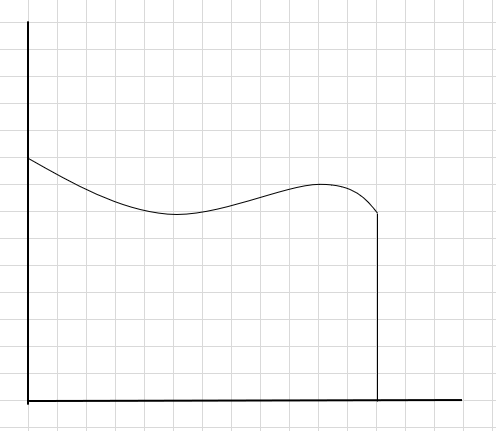
Один із способів – розділити область на чотири сегменти, а потім намалювати прямокутник (використовуючи цю лінію сегмента) так, щоб верхній правий кут кожного прямокутника торкався кривої (як показано нижче)
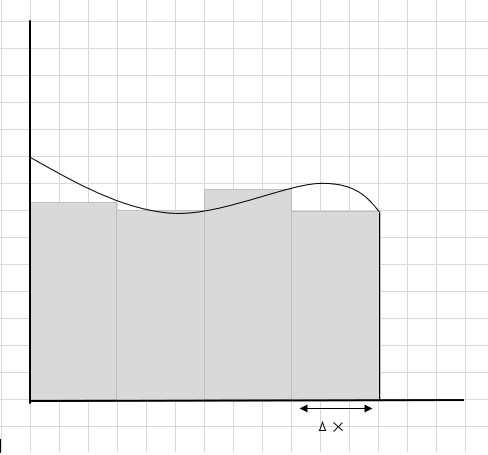
Сума площ цих прямокутних сегментів є оціночною площею під цією кривою. \(\Delta x \) — це ширина прямокутників/зрізів. Що ви думаєте про орієнтовну площу?
Багато частин кривої пропускається, і кілька додаткових частин враховуються під час обчислення площі цієї області кривої. Темно-сіра область зображення під реєстрацією означає втрачені та додаткові частини.
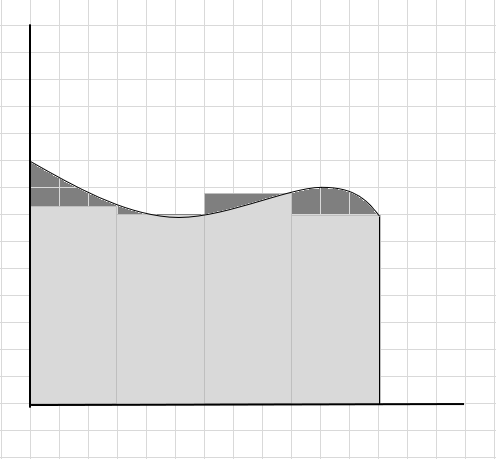
Ми можемо сказати, що це погана оцінка площі викривленої області, оскільки прямокутники не точно підходять під криву. Давайте розділимо площу під цією кривою на менші сегменти.
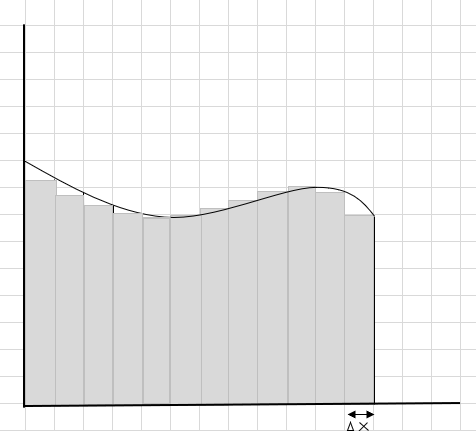
Ви бачите, що ці прямокутники вписуються всередину вигнутої області краще, ніж більші прямокутні сегменти. Давайте спробуємо розділити цю вигнуту область на менші сегменти/зрізи та спробуємо визначити площу під кривою.
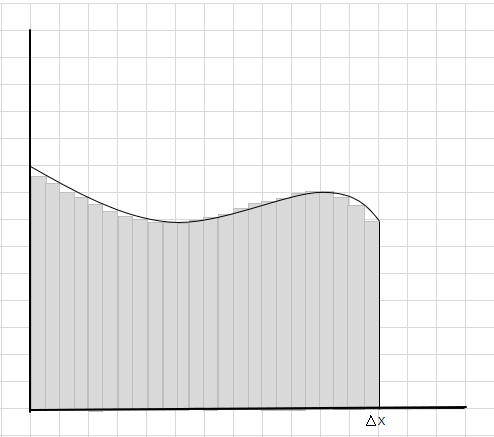
Пропущені та додаткові частини поступово зменшуються, а прямокутники набагато краще вписуються в область кривої. Ми можемо зробити висновок, що сума площ усіх цих прямокутників дає хорошу оцінку площі під кривою. Іншими словами, ми можемо сказати, що коли ширина зрізів наближається до нуля, відповідь наближається до істинної відповіді. Тепер ми пишемо dx для \(\Delta x\) щоб означати, що ширина наближається до нуля.
Давайте виведемо формулу для інтегрального числення тут:
Припустимо, нам потрібно знайти площу під цією кривою між точками a і b: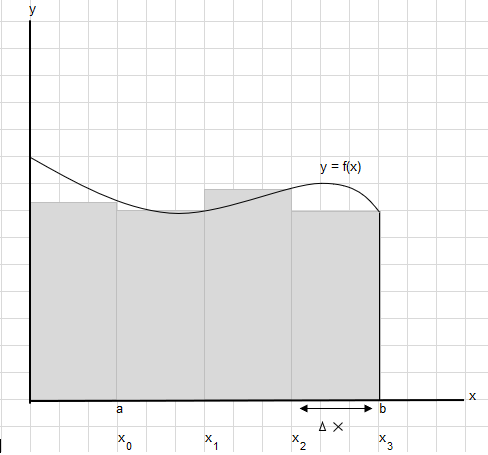
Розділіть площу між a і b на рівні сегменти так, щоб ширина кожного прямокутника була \(\Delta x\) .
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
Суму площ цих прямокутників можна записати як \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) .
Ми можемо мати кращу апроксимацію площі, коли \(\Delta x \) стає меншим або, іншими словами, коли кількість сегментів збільшується. Отже, \(\Delta x \) стає все тоншим і тоншим, а n стає все більшим і більшим. Це поняття отримання кращого наближення, оскільки ми беремо межу, коли n наближається до нескінченності та \(\Delta x \) стає нескінченно малим, є інтегралом.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) представляє площу під f від x між x = a і x = b
Знаходження інтеграла є зворотним до пошуку похідних.
Похідна x 2 дорівнює 2x. Отже, інтеграл від 2x дорівнює x 2 .
\(\int 2x \space dx = x^2 + C\) , де C — константа. Оскільки похідна константи дорівнює 0, отже, похідна від x 2 , x 2 +4, x 2 +10, x 2 +99 дорівнює 2x. Тому інтеграл від 2x дорівнює x 2 +C.
Розглянемо інтеграли загальних функцій:
| Загальні функції | функція | Інтеграл |
| Постійний | \(\int a \cdot dx\) | \(ax + c\) |
| змінна | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Майдан | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| Експоненціальний | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Тригонометрія (x у радіанах) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Загальні правила інтеграції:
| правила | функція | Інтеграл |
| Множення на константу | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Правило ступеня (n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Правило суми | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Правило різниці | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Класи інтегралів
\(\int f(x) \space dx\) представляє невизначений інтеграл, а \(\int_a^bf(x) \cdot dx\) представляє визначений інтеграл. Певний інтеграл має початкове та кінцеве значення. Тут a і b називаються межами або границями. Невизначений інтеграл є більш загальною формою інтегрування і може бути інтерпретований як антипохідна функції.
Ми знаходимо визначений інтеграл, обчислюючи невизначений інтеграл в точках a і b , а потім віднімаючи. Зрозуміємо це на прикладі:
Ми знаємо \(\int 2x \cdot dx = x^2 + C\) . Яким буде значення певного інтеграла \(\int _1^2 2x \cdot dx \) ?
При x =1 \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
При x = 2 \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
Відніміть (4 + C) - (1 + C) = 3
Значення \(\int _1^2 2x \cdot dx \) = 3