آپ سیکھیں گے:
مشتقات کے ساتھ انٹیگرلز کیلکولس میں بنیادی اشیاء ہیں۔ انٹیگرل کمپیوٹنگ کے عمل کو انضمام کہا جاتا ہے اور انٹیگرل کی تخمینی گنتی کو عددی انضمام کہا جاتا ہے۔
انٹیگرلز کی دو کلاسیں ہیں - definite integral (جیسے 5) اور Indefinite integrals، جن کی نچلی اور اوپری حد ہوتی ہے جیسے \(\int_a^bf(x) \cdot dx\) ۔
انٹیگرل کیا ہے؟
آئیے کہتے ہیں کہ ہمیں وکر کے نیچے کا رقبہ اور اوپر والے ایکس محور کو تلاش کرنا ہے۔
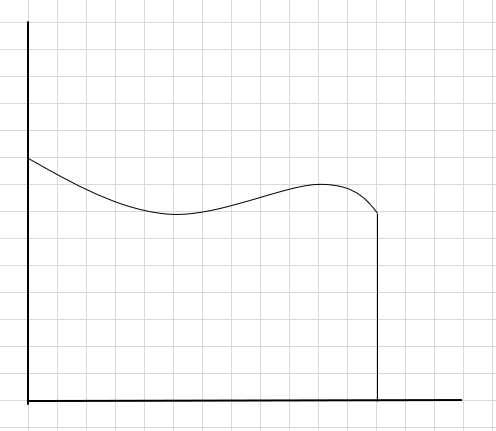
ایسا کرنے کا ایک طریقہ یہ ہے کہ خطے کو چار حصوں میں تقسیم کریں اور پھر ایک مستطیل کھینچیں (اس سیگمنٹ لائن کا استعمال کرتے ہوئے) اس طرح کہ ہر مستطیل کا اوپری دائیں کونا وکر کو چھوئے (جیسا کہ نیچے دیا گیا ہے)
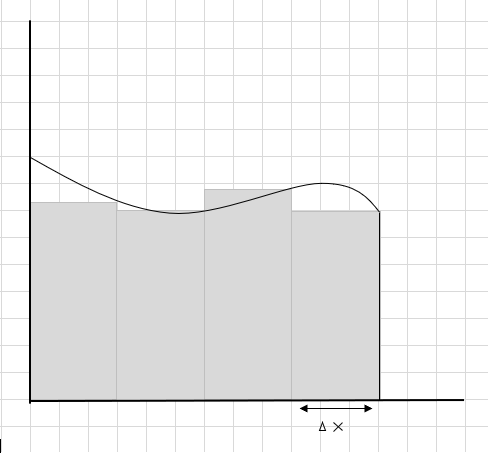
ان مستطیل حصوں کے رقبے کا مجموعہ اس منحنی خطوط کے نیچے کا تخمینہ شدہ رقبہ ہے۔ \(\Delta x \) مستطیل/سلائسز کی چوڑائی ہے۔ تخمینہ شدہ علاقے کے بارے میں آپ کا کیا خیال ہے؟
اس منحنی خطہ کے رقبے کا حساب لگاتے ہوئے بہت سارے منحنی حصے کو یاد کیا جاتا ہے اور کچھ اضافی حصوں پر غور کیا جاتا ہے۔ نیچے دی گئی تصویر میں چیک ان گہرا سرمئی خطہ مس آؤٹ اور اضافی حصوں کی نمائندگی کرتا ہے۔
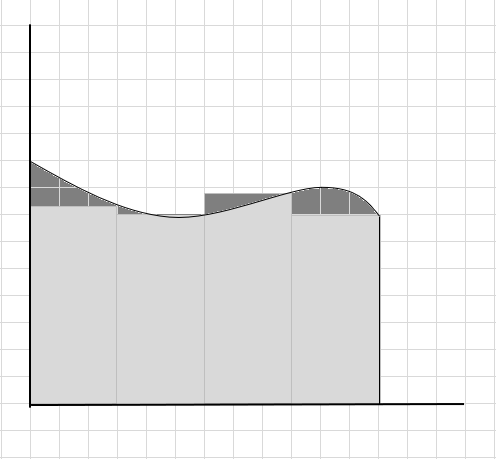
ہم کہہ سکتے ہیں کہ یہ منحنی خطہ کے رقبے کا ناقص تخمینہ ہے کیونکہ مستطیل وکر کے نیچے بالکل فٹ نہیں ہوتے ہیں۔ آئیے اس وکر کے نیچے کے علاقے کو چھوٹے حصوں میں تقسیم کرتے ہیں۔
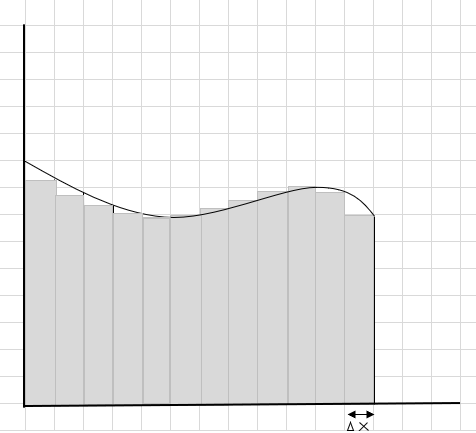
آپ دیکھ سکتے ہیں کہ یہ مستطیلیں بڑے مستطیل حصوں کی نسبت خمیدہ حصے کے اندر فٹ بیٹھتی ہیں۔ آئیے اس منحنی خطہ کو چھوٹے حصوں/سلائسز میں تقسیم کرنے کی کوشش کریں اور وکر کے نیچے کے علاقے کا تعین کرنے کی کوشش کریں۔
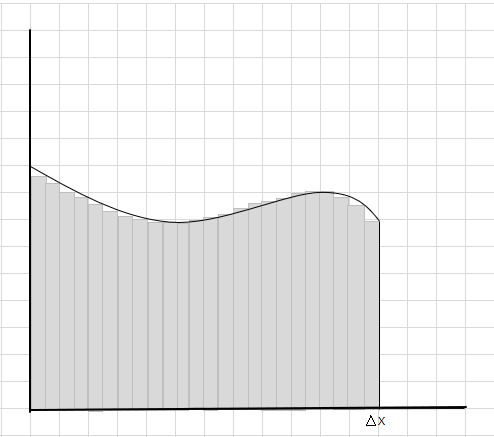
مس اور اضافی حصے بتدریج کم ہو رہے ہیں اور مستطیل منحنی خطہ کے اندر بہت بہتر فٹ ہو رہے ہیں۔ ہم اندازہ لگا سکتے ہیں کہ ان تمام مستطیلوں کے رقبے کا مجموعہ منحنی خطوط کے نیچے کے رقبے کا ایک اچھا تخمینہ دیتا ہے۔ یا دوسرے لفظوں میں، ہم کہہ سکتے ہیں جیسے ہی سلائسز چوڑائی میں صفر تک پہنچتے ہیں جواب سچے جواب کے قریب پہنچ جاتا ہے۔ اب ہم \(\Delta x\) کے لیے dx لکھتے ہیں اس کا مطلب ہے کہ چوڑائی صفر کے قریب پہنچ رہی ہے۔
آئیے یہاں انٹیگرل کیلکولس کا فارمولہ اخذ کرتے ہیں:
آئیے کہتے ہیں کہ ہمیں نقطہ a اور b کے درمیان اس وکر کے نیچے کا علاقہ تلاش کرنے کی ضرورت ہے: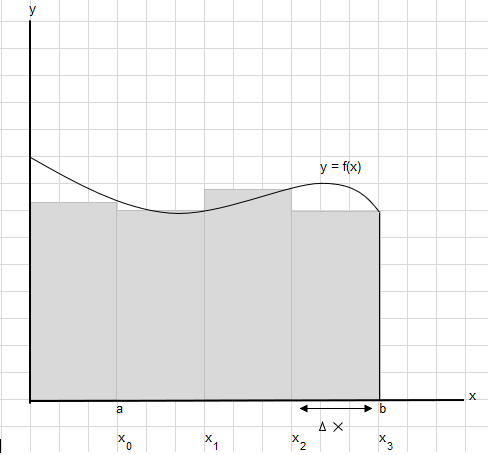
a اور b کے درمیان کے علاقے کو برابر حصوں میں تقسیم کریں کہ ہر مستطیل کی چوڑائی \(\Delta x\) ہو۔
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
ان مستطیلوں کے رقبے کا مجموعہ \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) کے طور پر لکھا جا سکتا ہے۔
ہم رقبہ کا بہتر تخمینہ لگا سکتے ہیں کیونکہ \(\Delta x \) چھوٹا ہو جاتا ہے یا دوسرے لفظوں میں جب کئی حصوں میں اضافہ ہوتا ہے۔ تو \(\Delta x \) پتلا اور پتلا ہوتا جاتا ہے اور n بڑا اور بڑا ہوتا جاتا ہے۔ بہتر قربت حاصل کرنے کا یہ تصور جب ہم حد کو n انفینٹی کے قریب پہنچتے ہیں اور \(\Delta x \) لامحدود طور پر چھوٹا ہوتا ہے تو یہ انٹیگرل ہے۔
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) = \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) x = a اور x = b کے درمیان x کے f کے نیچے کے علاقے کی نمائندگی کرتا ہے
انٹیگرل تلاش کرنا مشتقات کو تلاش کرنے کے الٹ ہے۔
x 2 کا مشتق 2x ہے۔ تو 2x کا انٹیگرل x 2 ہے۔
\(\int 2x \space dx = x^2 + C\) ، جہاں C ایک مستقل ہے۔ چونکہ مستقل کا مشتق 0 ہے لہذا x 2 ، x 2 +4، x 2 +10، x 2 +99 کا مشتق 2x ہے۔ لہذا 2x کا انٹیگرل x 2 +C ہے۔
آئیے عام افعال کے انضمام کو دیکھتے ہیں:
| عام افعال | فنکشن | لازمی |
| مستقل | \(\int a \cdot dx\) | \(ax + c\) |
| متغیر | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| مربع | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| کفایتی | \(\int e^x \cdot dx\) | \(e^x + c\) |
| مثلثیات (x ریڈین میں) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
عام انضمام کے اصول:
| قواعد | فنکشن | لازمی |
| ضرب بذریعہ مستقل | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| پاور رول (n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Sum Rule | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| فرق کا اصول | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
انٹیگرلز کی کلاسز
\(\int f(x) \space dx\) غیر معینہ انٹیگرل کی نمائندگی کرتا ہے اور \(\int_a^bf(x) \cdot dx\) ایک قطعی انٹیگرل کی نمائندگی کرتا ہے۔ ایک یقینی انٹیگرل کی شروعات اور اختتامی قدریں ہوتی ہیں۔ یہاں a اور b کو حدود یا حدود کہتے ہیں۔ indefinite integral انضمام کی ایک عمومی شکل ہے اور اسے فعل کے مخالف مشتق سے تعبیر کیا جا سکتا ہے۔
ہم غیر معینہ انٹیگرل کا حساب لگا کر a ، اور b پر، پھر گھٹا کر حاصل کرتے ہیں۔ آئیے اسے ایک مثال سے سمجھتے ہیں:
ہم جانتے ہیں \(\int 2x \cdot dx = x^2 + C\) ۔ ایک قطعی انٹیگرل کی قدر کیا ہوگی \(\int _1^2 2x \cdot dx \) ؟
x =1 پر، \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
x = 2 پر، \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
گھٹائیں (4 + C) - (1 + C) = 3
قدر \(\int _1^2 2x \cdot dx \) = 3