Siz o'rganasiz:
Integrallar hosilalar bilan birgalikda hisobning asosiy ob'ektlari hisoblanadi. Integralni hisoblash jarayoni integrallash , integralni taxminiy hisoblash esa sonli integrasiya deb ataladi.
Integrallarning ikkita klassi mavjud - aniq integral (5 kabi) va \(\int_a^bf(x) \cdot dx\) kabi pastki va yuqori chegaralariga ega bo'lgan noaniq integrallar.
Integral nima?
Aytaylik, egri chiziq ostidagi maydonni va yuqoridagi x o'qini topishimiz kerak.
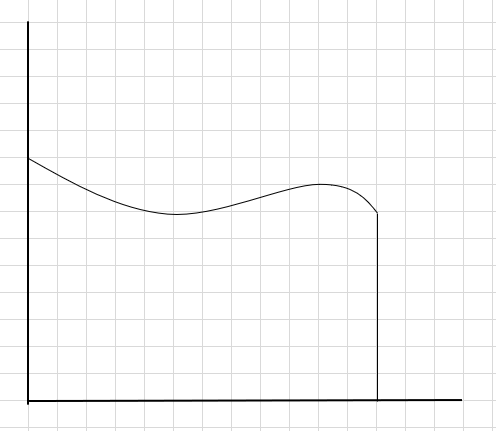
Buning usullaridan biri mintaqani to'rtta segmentga bo'lish va keyin har bir to'rtburchakning yuqori o'ng burchagi egri chiziqqa tegib turishi uchun to'rtburchak chizish (ushbu segment chizig'idan foydalanish)dir (quyida keltirilgan).
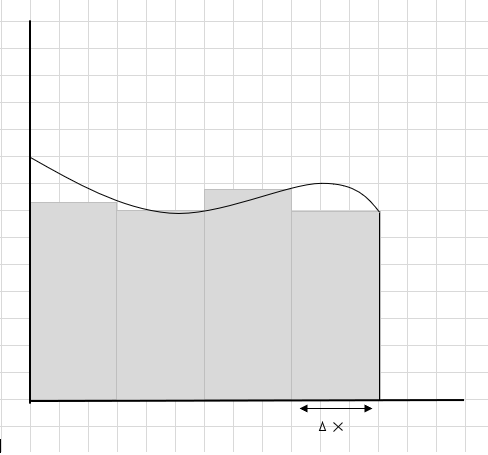
Ushbu to'rtburchaklar segmentlar maydonining yig'indisi ushbu egri chiziq ostidagi taxminiy maydondir. \(\Delta x \) - to'rtburchaklar/tilimlarning kengligi. Hisoblangan maydon haqida nima deb o'ylaysiz?
Egri chiziqning ko'p qismi o'tkazib yuborilgan va bu egri mintaqaning maydonini hisoblashda bir nechta qo'shimcha qismlar hisobga olinadi. Quyidagi rasmda roʻyxatdan oʻtish toʻq kulrang hudud oʻtkazib yuborilgan va qoʻshimcha qismlarni bildiradi.
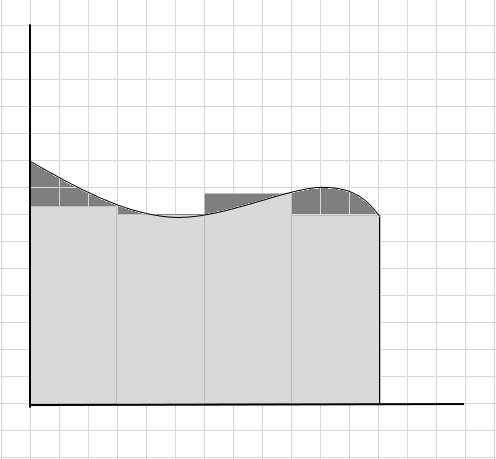
Aytishimiz mumkinki, bu egri chiziqning maydonini noto'g'ri baholash, chunki to'rtburchaklar egri chiziq ostiga to'liq mos kelmaydi. Keling, bu egri chiziq ostidagi maydonni kichikroq segmentlarga ajratamiz.
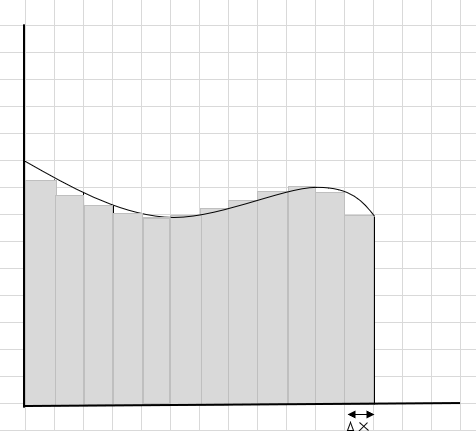
Ushbu to'rtburchaklar kattaroq to'rtburchaklar segmentlarga qaraganda egri maydon ichiga yaxshiroq mos kelishini ko'rishingiz mumkin. Keling, bu kavisli hududni kichikroq segmentlarga/bo'laklarga bo'lib, egri chiziq ostidagi maydonni aniqlashga harakat qilaylik.
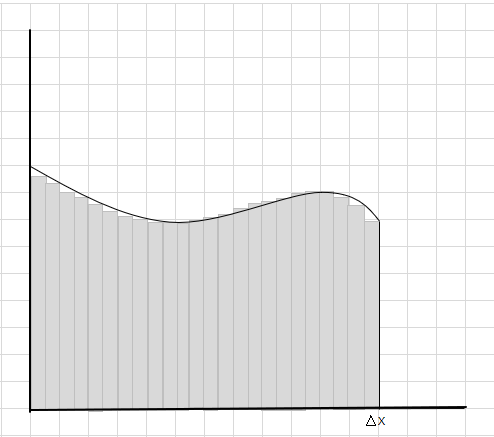
O'tkazib yuborilgan va qo'shimcha qismlar asta-sekin kamayib bormoqda va to'rtburchaklar egri mintaqaga ancha yaxshi mos tushadi. Biz bu to'rtburchaklar maydonining yig'indisi egri chiziq ostidagi maydonni yaxshi baholaydi, degan xulosaga kelishimiz mumkin. Yoki boshqacha qilib aytganda, biz tilimlarning kengligi nolga yaqinlashganda, javob haqiqiy javobga yaqinlashadi, deyishimiz mumkin. Endi \(\Delta x\) uchun dx ni yozamiz, bu kenglik nolga yaqinlashayotganini bildiradi.
Bu yerda integral hisob formulasini chiqaramiz:
Aytaylik, a va b nuqtalari orasidagi bu egri chiziq ostidagi maydonni topishimiz kerak: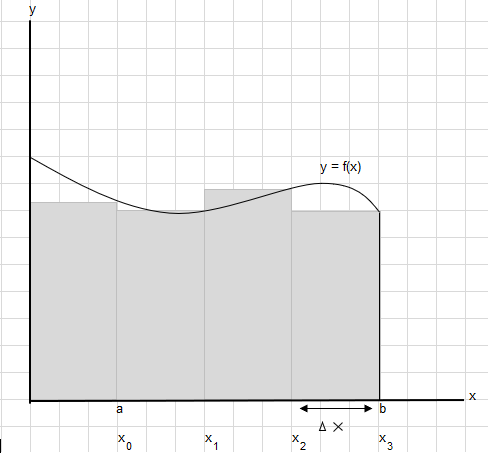
a va b orasidagi maydonni har bir to'rtburchakning kengligi \(\Delta x\) bo'lishi uchun teng segmentlarga ajrating.
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
Ushbu to'rtburchaklar maydoni yig'indisi \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) shaklida yozilishi mumkin.
Biz maydonni yaxshiroq yaqinlashtirishimiz mumkin, chunki \(\Delta x \) kichrayadi yoki boshqacha qilib aytganda, segmentlar soni ko'payganda. Shunday qilib \(\Delta x \) yupqaroq va ingichka bo'ladi va n kattaroq va kattaroq bo'ladi. n cheksizlikka yaqinlashganda va \(\Delta x \) cheksiz kichik bo'lib qolganda chegarani qabul qilganimizda, yaqinroq bo'lish haqidagi bu tushuncha Integraldir.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) x = a va x = b oralig'ida x ning f ostidagi maydonni ifodalaydi.
Integralni topish hosilalarni topishning teskarisidir.
X 2 ning hosilasi 2x. Demak, 2x ning integrali x 2 ga teng.
\(\int 2x \space dx = x^2 + C\) , bu erda C doimiydir. Doimiyning hosilasi 0 bo'lgani uchun x 2 , x 2 +4, x 2 +10, x 2 +99 ning hosilasi 2x bo'ladi. Shuning uchun 2x ning integrali x 2 +C ga teng.
Keling , umumiy funktsiyalarning integrallarini ko'rib chiqaylik:
| Umumiy funktsiyalar | Funktsiya | Integral |
| Doimiy | \(\int a \cdot dx\) | \(ax + c\) |
| O'zgaruvchan | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Kvadrat | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| Eksponensial | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Trigonometriya (radianlarda x) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Umumiy integratsiya qoidalari:
| Qoidalar | Funktsiya | Integral |
| Konstantaga ko'paytirish | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Quvvat qoidasi (n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Jamlama qoidasi | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Farq qoidasi | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Integrallar sinflari
\(\int f(x) \space dx\) noaniq integralni, \(\int_a^bf(x) \cdot dx\) esa aniq integralni ifodalaydi. Aniq integral boshlang'ich va yakuniy qiymatlarga ega. Bu yerda a va b chegaralar yoki chegaralar deyiladi. Noaniq integral ko'proq integratsiyaning umumiy shakli bo'lib, funktsiyaning anti-hosilasi sifatida talqin qilinishi mumkin.
Aniq integralni a va b da noaniq integralni hisoblab, keyin ayirib topamiz. Buni misol bilan tushunamiz:
Biz bilamiz \(\int 2x \cdot dx = x^2 + C\) . Aniq integralning qiymati qanday bo'ladi \(\int _1^2 2x \cdot dx \) ?
x =1 da, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
x = 2 da, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
Ayirish (4 + C) - (1 + C) = 3
\(\int _1^2 2x \cdot dx \) qiymati = 3