Bạn sẽ học:
Tích phân cùng với đạo hàm là những đối tượng cơ bản trong giải tích. Quá trình tính toán một tích phân được gọi là tích phân và tính toán gần đúng của một tích phân được gọi là tích phân số.
Có hai loại tích phân - tích phân xác định (như 5) và tích phân không xác định, có giới hạn trên và dưới như \(\int_a^bf(x) \cdot dx\) .
Tích phân là gì?
Giả sử chúng ta phải tìm diện tích dưới đường cong và trục x ở trên.
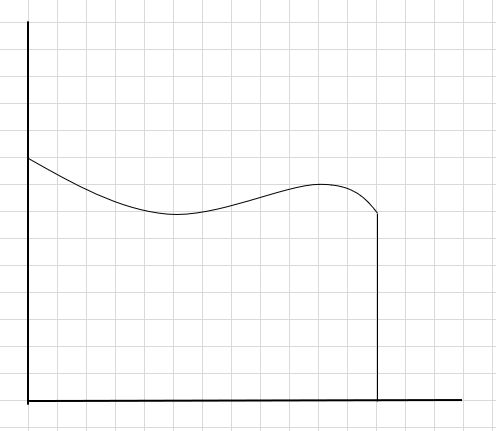
Một cách để làm là chia vùng thành bốn đoạn và sau đó vẽ một hình chữ nhật (sử dụng đường phân đoạn này) sao cho góc trên bên phải của mỗi hình chữ nhật chạm vào đường cong (như được đưa ra bên dưới)
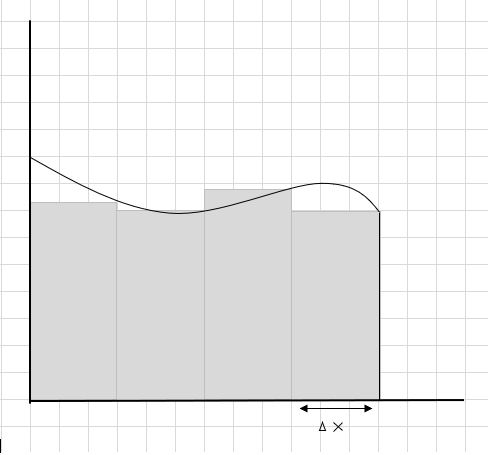
Tổng diện tích của các đoạn hình chữ nhật này là diện tích ước tính bên dưới đường cong này. \(\Delta x \) là chiều rộng của hình chữ nhật/lát. Bạn nghĩ gì về diện tích ước tính?
Rất nhiều phần đường cong bị bỏ qua và một vài phần bổ sung được xem xét khi tính diện tích của vùng đường cong này. Check-in bên dưới hình ảnh vùng màu xám đậm thể hiện phần bỏ sót và bổ sung.
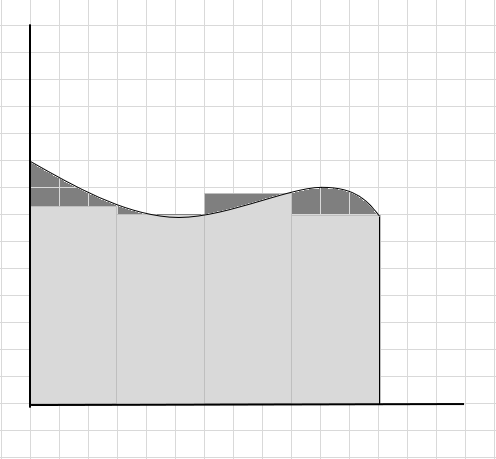
Có thể nói đây là một ước tính kém về diện tích của vùng cong vì hình chữ nhật không nằm chính xác dưới đường cong. Hãy chia khu vực dưới đường cong này thành các phần nhỏ hơn.
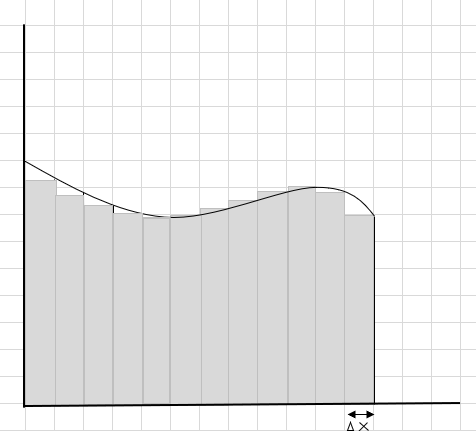
Bạn có thể thấy rằng những hình chữ nhật này nằm gọn trong vùng cong tốt hơn so với các đoạn hình chữ nhật lớn hơn. Hãy thử chia vùng cong này thành các đoạn/lát nhỏ hơn và cố gắng xác định vùng bên dưới đường cong.
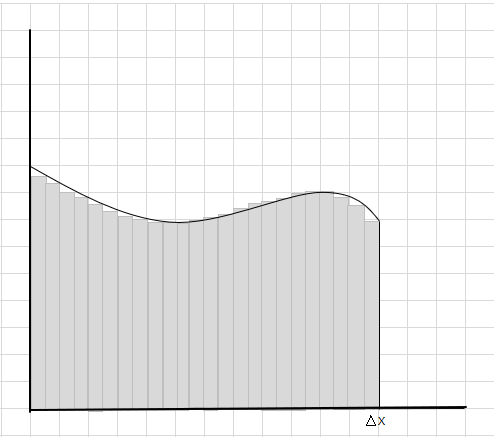
Phần bỏ lỡ và phần thừa đang giảm dần và hình chữ nhật vừa vặn hơn nhiều bên trong khu vực đường cong. Chúng ta có thể suy ra rằng tổng diện tích của tất cả các hình chữ nhật này đưa ra một ước tính tốt về diện tích dưới đường cong. Hay nói cách khác, chúng ta có thể nói khi các lát cắt có chiều rộng bằng 0 thì câu trả lời sẽ tiệm cận với câu trả lời đúng. Bây giờ chúng ta viết dx cho \(\Delta x\) để có nghĩa là chiều rộng đang tiến dần đến 0.
Hãy rút ra công thức tính tích phân ở đây:
Giả sử chúng ta cần tìm diện tích dưới đường cong này giữa điểm a và b: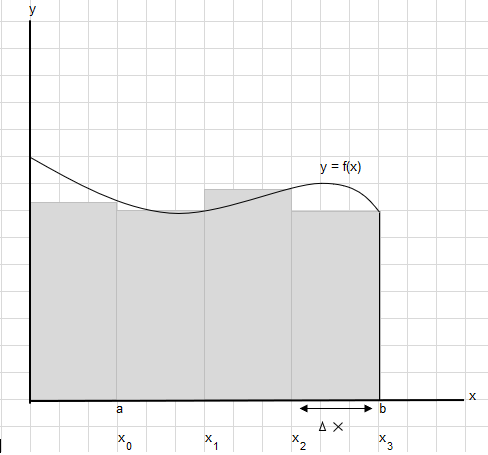
Chia diện tích giữa a và b thành các đoạn bằng nhau sao cho chiều rộng của mỗi hình chữ nhật là \(\Delta x\) .
\(x_1-x_0 = x_2-x_1=x_3-x_2 = \Delta x\)
Tổng diện tích của các hình chữ nhật này có thể được viết là \(\displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) .
Chúng ta có thể có diện tích gần đúng tốt hơn khi \(\Delta x \) nhỏ hơn hay nói cách khác khi số đoạn tăng lên. Vì vậy, \(\Delta x \) ngày càng mỏng hơn và n ngày càng lớn hơn. Khái niệm về việc đạt được giá trị gần đúng tốt hơn khi chúng ta lấy giới hạn khi n tiến đến vô cùng và \(\Delta x \) trở nên cực nhỏ là Tích phân.
\(\lim\limits_{n \to \infty} \displaystyle \sum_{i=1}^{n} f(x_i)\cdot\Delta x_i\) = \(\int_a^bf(x) \space dx\)
\(\int_a^bf(x) \space dx\) đại diện cho diện tích bên dưới f của x giữa x = a và x = b
Tìm Tích phân ngược lại với tìm Đạo hàm.
Đạo hàm của x 2 là 2x. Vậy tích phân của 2x là x 2 .
\(\int 2x \space dx = x^2 + C\) , trong đó C là hằng số. Vì đạo hàm của hằng số bằng 0 nên đạo hàm của x 2 , x 2 +4, x 2 +10, x 2 +99 là 2x. Do đó tích phân của 2x là x 2 +C.
Hãy xét tích phân của các hàm phổ biến:
| Chức năng phổ biến | Hàm số | tích phân |
| Hằng số | \(\int a \cdot dx\) | \(ax + c\) |
| Biến đổi | \(\int x \cdot dx\) | \(\frac{x^2}{2} + c\) |
| Quảng trường | \(\int x^2 \cdot dx\) | \(\frac{x^3}{3} + c\) |
| số mũ | \(\int e^x \cdot dx\) | \(e^x + c\) |
| Lượng giác(x tính bằng radian) | \(\int \cos(x) \cdot dx\) | \(\sin(x) + c\) |
| \(\int \sin(x) \cdot dx\) | \(-\cos(x) + c\) | |
| \(\int \sec^2(x) \cdot dx\) | \(\tan(x) + c\) |
Quy tắc tích hợp chung:
| Quy tắc | Hàm số | tích phân |
| Nhân với hằng số | \(\int cf(x) \cdot dx\) | \(c\int f(x) \cdot dx\) |
| Quy tắc lũy thừa(n <> -1) | \(\int x^n\cdot dx\) | \(\frac{x^{n+1}}{n+1} + C\) |
| Quy tắc tổng | \(\int (f+g)\cdot dx\) | \(\int f\cdot dx + \int g\cdot dx\) |
| Quy tắc khác biệt | \(\int (fg)\cdot dx\) | \(\int f\cdot dx - \int g\cdot dx\) |
Các lớp tích phân
\(\int f(x) \space dx\) đại diện cho tích phân bất định và \(\int_a^bf(x) \cdot dx\) đại diện cho tích phân xác định. Một tích phân xác định có giá trị đầu và cuối. Ở đây a và b được gọi là giới hạn hoặc ranh giới. Tích phân không xác định là một dạng tích phân tổng quát hơn và có thể được hiểu là phản đạo hàm của hàm.
Chúng ta tìm Tích phân xác định bằng cách tính Tích phân không xác định tại a , và tại b , sau đó trừ đi. Hãy để chúng tôi hiểu điều này bằng một ví dụ:
Chúng tôi biết \(\int 2x \cdot dx = x^2 + C\) . Giá trị của tích phân xác định \(\int _1^2 2x \cdot dx \) sẽ là bao nhiêu?
Tại x =1, \(\int 2x \cdot dx = 1^2 + C\) = 1 + C
Tại x = 2, \(\int 2x\cdot dx = 2^2 + C\) = 4 + C
Trừ (4 + C) - (1 + C) = 3
Giá trị của \(\int _1^2 2x \cdot dx \) = 3