سوف تتعلم:
مخطط Venn هو مخطط يوضح العلاقة بين المجموعات التي تشترك في شيء مشترك. تصور هذه المخططات العناصر كنقاط في مستوى ويتم تعيينها كمناطق داخل المنحنى المغلق (عادة ما تكون دائرة).
مخطط فين هو طريقة تخطيطية لتمثيل عناصر مجموعة أو مجموعة. الآن كما تعلمنا بالفعل مجموعة وخصائصها. دعنا نحاول تقديم المجموعات باستخدام مخطط Venn.
مثال: يوجد 10 طلاب في الفصل. التحق بعض الطلاب بفصول غير منهجية مثل الرسم والسباحة والموسيقى والرقص.
هنا مجموعة عالمية تمثل طلاب الفصل. المجموعة العامة هي مجموعة تحتوي على جميع الكائنات أو العناصر والتي تعتبر المجموعات الأخرى منها مجموعات فرعية.
U = {جون ، سام ، لي ، ماري ، فريد ، داني ، توم ، فين ، تيم ، تريسي}
مجموعة الطلاب الذين يحضرون فصل الرقص هي D = {John، Tim، Mary، Lee}؛ عدد العناصر في المجموعة D هو 4 ، \(n(D) = 4\)
مجموعة الطلاب الذين يحضرون فصل الموسيقى هم M = {Fred، Tracy، Tim، Danny، Tom}؛ عدد العناصر في المجموعة M هو 5 ، \(n(M) = 5\)
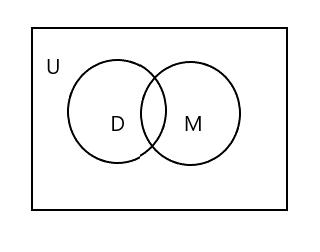
ستلاحظ أنه في مخطط Venn أعلاه ، يمثل U المنطقة المستطيلة بأكملها. يتم تمثيل مجموعة D و M بواسطة الدوائر. الدائرتان متقاطعتان لأن لديهما القليل من العناصر المشتركة. هنا "تيم" عنصر مشترك في كلتا المجموعتين.
يمثل تقاطع المجموعات العناصر المشتركة في كلتا المجموعتين ويُشار إليه بالرمز ' \(\cap\) '.
الجزء المظلل في الرسم البياني أدناه يمثل \(D \cap M\)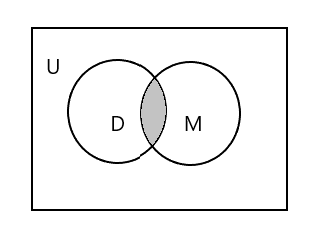
\(D \cap M = \) {Tim}
\(n(D \cap M) = 1\)
لنفترض أننا نريد سرد جميع الطلاب الذين يحضرون الرقص أو الموسيقى أو كليهما.
اتحاد مجموعتين معينتين هو أصغر مجموعة تحتوي على جميع عناصر كلتا المجموعتين. يشار إليه بالرمز "U". الجزء المظلل في الرسم البياني أدناه يمثل \(D \cup M\)
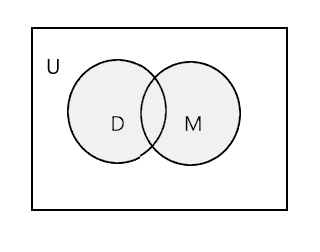
\(D \cup M =\) {جون ، تيم ، ماري ، لي ، فريد ، تريسي ، داني ، توم}
\(n(D \cup M) = 8\)
يمكنك أيضًا طرح مجموعة من مجموعة أخرى. هنا سيمثل D - M مجموعة الطلاب الذين يحضرون الرقص وليس الموسيقى.
\(D − M = \) {جون ، ماري ، لي}
\(n(D - M) = 3\)
يمثل الجزء المظلل في مخطط Venn أدناه D - M:
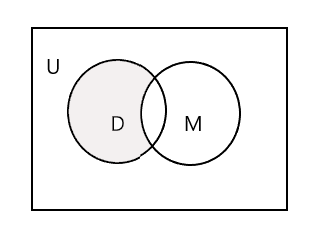
لنأخذ المجموعة الثالثة ، مجموعة من الطلاب الذين يحضرون فصل الرسم. P = {John و Sam و Danny و Tracy} و n (P) = 4
مخطط Venn لتمثيل المجموعات الثلاث جميعها:
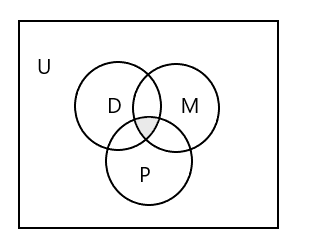
كيف تمثل مجموعة الطلاب الذين يحضرون جميع الفصول الثلاثة؟
الجواب: \(D \cap M \cap P\) = {} ، حيث لا يوجد طالب يحضر جميع الفصول الثلاثة. انظر إلى الجزء المظلل في مخطط فين أعلاه.
كيف تمثل مجموعة الطلاب الذين يحضرون دروس الرقص والرسم؟
إجابه:
\(D \cap P =\) {جون}
\(n(D \cap P) = 1\)