Sən öyrənəcəksən:
Venn diaqramı , ortaq bir şeyi paylaşan çoxluqlar arasındakı əlaqəni göstərən diaqramdır. Bu diaqramlar elementləri müstəvidə nöqtələr kimi təsvir edir və qapalı əyrinin (adətən dairə) daxilində bölgələr kimi təyin edir.
Venn diaqramı çoxluğun və ya qrupun elementlərini təsvir etməyin sxematik üsuludur. Artıq çoxluğu və onun xassələrini öyrəndiyimiz kimi. Venn diaqramından istifadə edərək dəstləri təqdim etməyə çalışaq.
Misal: Bir sinifdə 10 şagird var. Bəzi tələbələr rəsm, üzgüçülük, musiqi və rəqs kimi sinifdənkənar dərslərə yazılıblar.
Burada Universal dəst sinif şagirdlərini təmsil edir. Universal çoxluq bütün obyektləri və ya elementləri ehtiva edən və digər çoxluqların alt çoxluqları olan çoxluqdur.
U = {Con, Sam, Lee, Mary, Fred, Denny, Tom, Venn, Tim, Tracy}
Rəqs dərsində iştirak edən tələbələr toplusu D = {Con, Tim, Mary, Lee} ; D çoxluğundakı elementlərin sayı 4-dür, \(n(D) = 4\)
Musiqi dərsində iştirak edən tələbələr dəsti M = {Fred, Tracy, Tim, Denny, Tom} ; M çoxluğundakı elementlərin sayı 5-dir, \(n(M) = 5\)
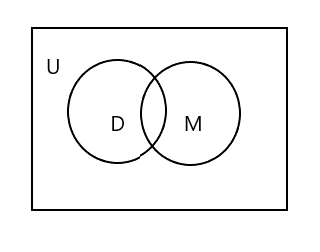
Yuxarıdakı Venn diaqramında U-nun bütün düzbucaqlı sahəni təmsil etdiyini görəcəksiniz. D və M çoxluğu dairələrlə təmsil olunur. İki dairə kəsişir, çünki onların ortaq elementləri azdır. Burada 'Tim' hər iki dəstdə ümumi elementdir.
Çoxluqların kəsişməsi hər iki çoxluqda ümumi olan elementləri təmsil edir və ' \(\cap\) ' simvolu ilə işarələnir.
Aşağıdakı diaqramdakı kölgəli hissə \(D \cap M\) ifadə edir.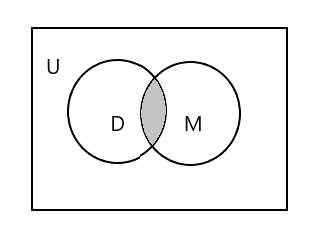
\(D \cap M = \) {Tim}
\(n(D \cap M) = 1\)
Tutaq ki, rəqs və ya musiqi və ya hər ikisində iştirak edən bütün tələbələri sadalamaq istəyirik.
Verilmiş iki çoxluğun birliyi hər iki çoxluğun bütün elementlərini özündə birləşdirən ən kiçik çoxluqdur. 'U' simvolu ilə işarələnir. Aşağıdakı diaqramdakı kölgəli hissə \(D \cup M\) ifadə edir.
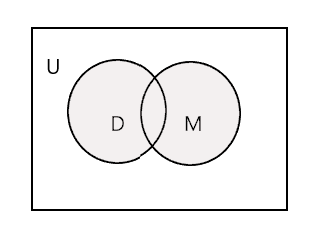
\(D \cup M =\) {Con, Tim, Mary, Li, Fred, Tracy, Denny, Tom}
\(n(D \cup M) = 8\)
Siz həmçinin bir dəsti digərindən çıxara bilərsiniz. Burada D - M musiqiyə deyil , rəqsə qatılan tələbələr toplusunu təmsil edəcək.
\(D − M = \) { Con, Meri, Li }
\(n(D - M) = 3\)
Aşağıdakı Venn diaqramındakı kölgəli hissə D - M-ni təmsil edir:
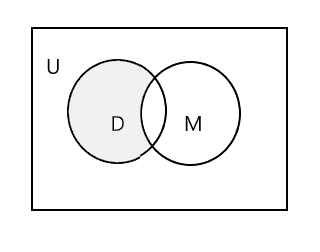
Gəlin üçüncü dəsti götürək, rəsm dərsində iştirak edən tələbələr toplusu. P = {Con, Sam, Denny, Tracy} və n(P) = 4
Hər üç dəsti təmsil etmək üçün Venn diaqramı:
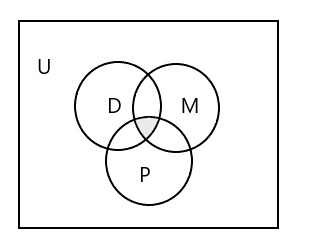
Hər üç dərsdə iştirak edən tələbələr toplusunu necə təmsil etmək olar?
Cavab: \(D \cap M \cap P\) = { }, çünki hər üç dərsdə heç bir tələbə iştirak etmir. Yuxarıdakı Venn diaqramında kölgəli hissəyə baxın.
Rəqs və rəsm dərsinə qatılan tələbələr toplusunu necə təmsil etmək olar?
Cavab:
\(D \cap P =\) {John}
\(n(D \cap P) = 1\)