তুমি শিখবে:
একটি ভেন ডায়াগ্রাম হল একটি ডায়াগ্রাম যা সাধারণ কিছু ভাগ করে এমন সেটগুলির মধ্যে এবং মধ্যে সম্পর্ক দেখায়। এই চিত্রগুলি একটি সমতলের বিন্দু হিসাবে উপাদানগুলিকে চিত্রিত করে এবং বন্ধ বক্ররেখার (সাধারণত একটি বৃত্ত) ভিতরে অঞ্চল হিসাবে সেট করে।
ভেন ডায়াগ্রাম হল একটি সেট বা গ্রুপের উপাদানগুলিকে উপস্থাপন করার একটি পরিকল্পিত উপায়। এখন আমরা ইতিমধ্যে সেট এবং এর বৈশিষ্ট্য শিখেছি। আসুন ভেন ডায়াগ্রাম ব্যবহার করে সেট উপস্থাপন করার চেষ্টা করি।
উদাহরণ: একটি ক্লাসে 10 জন ছাত্র আছে। কিছু শিক্ষার্থী পেইন্টিং, সাঁতার, সঙ্গীত এবং নৃত্যের মতো পাঠ্যক্রম বহির্ভূত ক্লাসে নিজেদের নাম নথিভুক্ত করেছে।
এখানে ইউনিভার্সাল সেট ক্লাসের ছাত্রদের প্রতিনিধিত্ব করে। ইউনিভার্সাল সেট হল এমন একটি সেট যাতে সমস্ত বস্তু বা উপাদান থাকে এবং যার মধ্যে অন্যান্য সেটগুলি উপসেট।
U = {জন, স্যাম, লি, মেরি, ফ্রেড, ড্যানি, টম, ভেন, টিম, ট্রেসি}
নাচের ক্লাসে অংশগ্রহণকারী ছাত্রদের সেট হল D = {জন, টিম, মেরি, লি} ; D সেটে উপাদানের সংখ্যা 4, \(n(D) = 4\)
মিউজিক ক্লাসে অংশগ্রহণকারী ছাত্রদের সেট হল M = {ফ্রেড, ট্রেসি, টিম, ড্যানি, টম} ; সেট M এ উপাদানের সংখ্যা 5, \(n(M) = 5\)
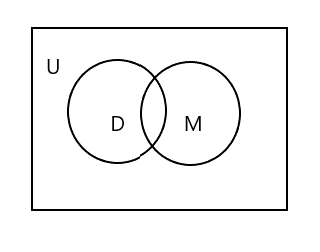
আপনি লক্ষ্য করবেন যে উপরের ভেন ডায়াগ্রামে U সমগ্র আয়তক্ষেত্রাকার এলাকাকে প্রতিনিধিত্ব করছে। D এবং M সেট বৃত্ত দ্বারা প্রতিনিধিত্ব করা হয়। দুটি বৃত্ত ছেদ করছে কারণ তাদের মধ্যে কয়েকটি উপাদান মিল রয়েছে। এখানে উভয় সেটে 'টিম' একটি সাধারণ উপাদান।
সেটগুলির ছেদ এমন উপাদানগুলিকে উপস্থাপন করে যা উভয় সেটেই সাধারণ এবং ' \(\cap\) ' চিহ্ন দ্বারা চিহ্নিত করা হয়।
নীচের চিত্রের ছায়াযুক্ত অংশটি প্রতিনিধিত্ব করে \(D \cap M\)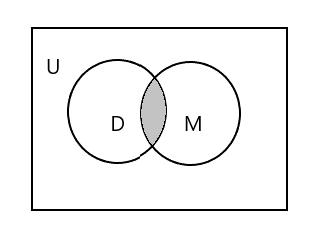
\(D \cap M = \) {টিম}
\(n(D \cap M) = 1\)
ধরুন আমরা এমন সমস্ত ছাত্রদের তালিকা করতে চাই যারা নাচ বা সঙ্গীত বা উভয়ই হয়।
প্রদত্ত দুটি সেটের ইউনিয়ন হল ক্ষুদ্রতম সেট যা উভয় সেটের সমস্ত উপাদান ধারণ করে। এটি 'U' চিহ্ন দ্বারা চিহ্নিত করা হয়। নীচের চিত্রের ছায়াযুক্ত অংশটি প্রতিনিধিত্ব করে \(D \cup M\)
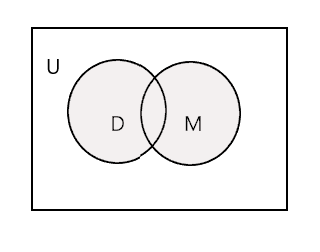
\(D \cup M =\) {জন, টিম, মেরি, লি, ফ্রেড, ট্রেসি, ড্যানি, টম}
\(n(D \cup M) = 8\)
আপনি একটি সেট থেকে অন্য সেট বিয়োগও করতে পারেন। এখানে D - M ছাত্রদের সেটের প্রতিনিধিত্ব করবে যারা নাচে অংশ নেয় কিন্তু সঙ্গীত নয় ।
\(D − M = \) { জন, মেরি, লি }
\(n(D - M) = 3\)
নীচের ভেন ডায়াগ্রামে ছায়াযুক্ত অংশটি D - M প্রতিনিধিত্ব করে:
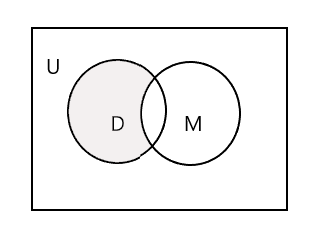
আসুন তৃতীয় সেটটি নেওয়া যাক, ছাত্রদের একটি সেট যারা পেইন্টিং ক্লাসে অংশ নেয়। P = {জন, স্যাম, ড্যানি, ট্রেসি} এবং n(P) = 4
তিনটি সেটের প্রতিনিধিত্ব করার জন্য ভেন ডায়াগ্রাম:
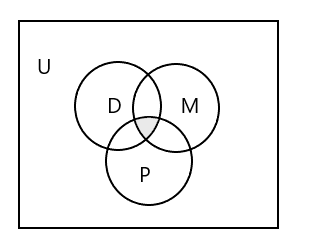
তিনটি ক্লাসে উপস্থিত ছাত্রদের সেটকে কীভাবে প্রতিনিধিত্ব করবেন?
উত্তর: \(D \cap M \cap P\) = { }, যেহেতু কোনো শিক্ষার্থী তিনটি ক্লাসেই উপস্থিত হয় না। উপরের ভেন ডায়াগ্রামে ছায়াযুক্ত অংশটি দেখুন।
নাচ এবং চিত্রকলার ক্লাসে অংশগ্রহণকারী শিক্ষার্থীদের সেটকে কীভাবে প্রতিনিধিত্ব করবেন?
উত্তর:
\(D \cap P =\) {জন}
\(n(D \cap P) = 1\)