Du wirst es lernen:
Ein Venn-Diagramm ist ein Diagramm, das die Beziehung zwischen und zwischen Mengen zeigt, die etwas gemeinsam haben. Diese Diagramme zeigen Elemente als Punkte in einer Ebene und Mengen als Bereiche innerhalb der geschlossenen Kurve (normalerweise ein Kreis).
Das Venn-Diagramm ist eine schematische Darstellung der Elemente einer Menge oder Gruppe. Nun, wie wir bereits gelernt haben, set und seine Eigenschaften. Versuchen wir, Mengen mithilfe des Venn-Diagramms darzustellen.
Beispiel: In einer Klasse sind 10 Schüler. Einige Schüler haben sich für außerschulische Kurse wie Malen, Schwimmen, Musik und Tanz angemeldet.
Hier repräsentiert das Universal-Set die Schüler der Klasse. Die universelle Menge ist eine Menge, die alle Objekte oder Elemente enthält und von der andere Mengen Teilmengen sind.
U = {John, Sam, Lee, Mary, Fred, Danny, Tom, Venn, Tim, Tracy}
Gruppe von Schülern, die den Tanzkurs besuchen, ist D = {John, Tim, Mary, Lee} ; Anzahl der Elemente in Menge D ist 4, \(n(D) = 4\)
Gruppe von Schülern, die den Musikunterricht besuchen, ist M = {Fred, Tracy, Tim, Danny, Tom} ; Anzahl der Elemente in Menge M ist 5, \(n(M) = 5\)
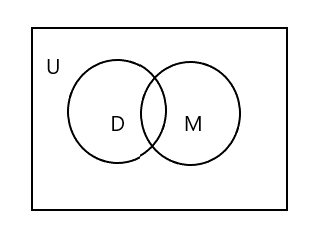
Sie werden feststellen, dass U im obigen Venn-Diagramm die gesamte rechteckige Fläche darstellt. D- und M-Satz sind durch Kreise dargestellt. Die beiden Kreise schneiden sich, da sie nur wenige Elemente gemeinsam haben. Hier ist „Tim“ ein gemeinsames Element in beiden Sets.
Der Schnittpunkt von Mengen stellt Elemente dar, die in beiden Mengen gemeinsam sind, und wird durch das Symbol ' \(\cap\) ' bezeichnet.
Der schattierte Teil im Diagramm unten repräsentiert \(D \cap M\)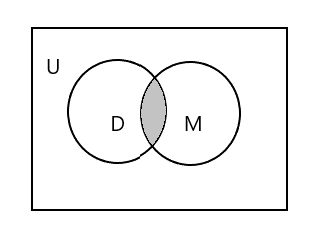
\(D \cap M = \) {Tim}
\(n(D \cap M) = 1\)
Angenommen, wir möchten alle Schüler auflisten, die entweder Tanz oder Musik oder beides besuchen.
Die Vereinigung zweier gegebener Mengen ist die kleinste Menge, die alle Elemente beider Mengen enthält. Es ist mit dem Symbol „U“ gekennzeichnet. Der schattierte Teil im folgenden Diagramm repräsentiert \(D \cup M\)
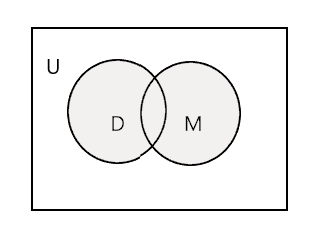
\(D \cup M =\) {John, Tim, Mary, Lee, Fred, Tracy, Danny, Tom}
\(n(D \cup M) = 8\)
Sie können auch einen Satz von einem anderen subtrahieren . Hier repräsentiert D - M die Gruppe von Studenten, die Tanz, aber keine Musik besuchen.
\(D − M = \) { John, Mary, Lee }
\(n(D - M) = 3\)
Der schattierte Teil im folgenden Venn-Diagramm stellt D - M dar:
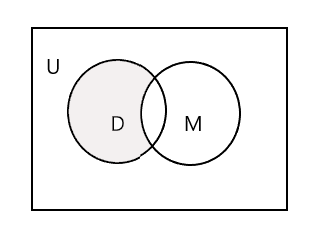
Nehmen wir die dritte Gruppe, eine Gruppe von Schülern, die den Malunterricht besuchen. P = {John, Sam, Danny, Tracy} und n(P) = 4
Venn-Diagramm zur Darstellung aller drei Sätze:
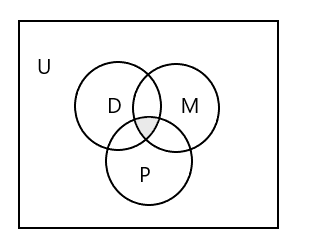
Wie stellt man die Schülergruppe dar, die alle drei Klassen besucht?
Antwort: \(D \cap M \cap P\) = { }, da kein Schüler alle drei Klassen besucht. Sehen Sie sich den schraffierten Teil im obigen Venn-Diagramm an.
Wie stellt man die Gruppe der Schüler dar, die den Tanz- und Malunterricht besuchen?
Antworten:
\(D \cap P =\) {Johannes}
\(n(D \cap P) = 1\)