You will learn:
A Venn diagram is a diagram that shows the relationship between and among sets that shares something in common. These diagrams depict elements as points in a plane and sets as regions inside the closed curve(usually a circle).
Venn diagram is a schematic way of representing the elements of a set or a group. Now as we already learnt set and its properties. Let's try to present sets using Venn diagram.
Example: There are 10 students in a class. Some students have enrolled themselves in extracurricular classes like painting, swimming, music and dance.
Here Universal set represents students of the class. The Universal set is a set containing all objects or elements and of which other sets are subsets.
U = {John, Sam, Lee, Mary, Fred, Danny, Tom, Venn, Tim, Tracy}
Set of students attending dance class is D = {John, Tim, Mary, Lee} ; Number of element in set D is 4, \(n(D) = 4\)
Set of students attending music class is M = {Fred, Tracy, Tim, Danny, Tom} ; Number of element in set M is 5, \(n(M) = 5\)
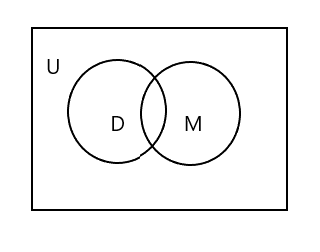
You will notice that in the above Venn diagram U is representing the whole rectangular area. D and M set are represented by circles. The two circles are intersecting as they have few elements in common. Here 'Tim' is a common element in both the sets.
The Intersection of sets represents elements that are common in both sets and is denoted by the symbol '\(\cap\)'.
The shaded portion in the diagram below represents \(D \cap M\)
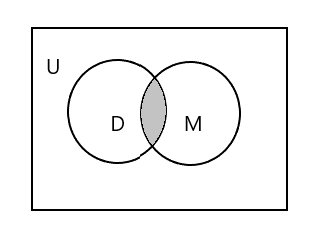
\(D \cap M = \) {Tim}
\(n(D \cap M) = 1\)
Suppose we want to list all students that attend either dance or music or both.
Union of two given sets is the smallest set which contains all the elements of both the sets. It is denoted by symbol 'U'. The shaded portion in the below diagram represents \(D \cup M\)
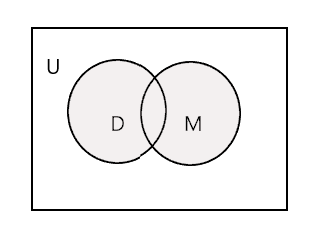
\(D \cup M =\) {John, Tim, Mary, Lee, Fred, Tracy, Danny, Tom}
\(n(D \cup M) = 8\)
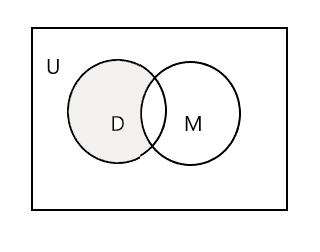
You can also subtract one set from another. Here D - M will represent the set of students that attend dance but not music.
\(D − M = \) { John, Mary, Lee }
\(n(D - M) = 3\)
The shaded portion in the below Venn diagram represents D - M :
Let's take the third set, a set of students who attend painting class. P = {John, Sam, Danny, Tracy} and n(P) = 4
Venn diagram to represent all three sets:
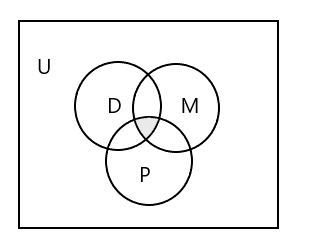
How to represent the set of students who attends all three classes?
Answer: \(D \cap M \cap P\) = { }, as no student attends all the three classes. Look at the shaded portion in the above Venn diagram.
How to represent the set of students who attends dance and painting class?
Answer:
\(D \cap P =\) {John}
\(n(D \cap P) = 1\)