Aprenderás:
Un diagrama de Venn es un diagrama que muestra la relación entre conjuntos que comparten algo en común. Estos diagramas representan elementos como puntos en un plano y conjuntos como regiones dentro de la curva cerrada (generalmente un círculo).
El diagrama de Venn es una forma esquemática de representar los elementos de un conjunto o grupo. Ahora como ya aprendimos el conjunto y sus propiedades. Intentemos presentar conjuntos usando el diagrama de Venn.
Ejemplo: Hay 10 estudiantes en una clase. Algunos estudiantes se han inscrito en clases extracurriculares como pintura, natación, música y danza.
Aquí el conjunto Universal representa a los estudiantes de la clase. El conjunto Universal es un conjunto que contiene todos los objetos o elementos y del cual otros conjuntos son subconjuntos.
U = {Juan, Sam, Lee, María, Fred, Danny, Tom, Venn, Tim, Tracy}
El conjunto de estudiantes que asisten a la clase de baile es D = {John, Tim, Mary, Lee}; El número de elementos en el conjunto D es 4, \(n(D) = 4\)
El conjunto de estudiantes que asisten a la clase de música es M = {Fred, Tracy, Tim, Danny, Tom}; El número de elementos en el conjunto M es 5, \(n(M) = 5\)
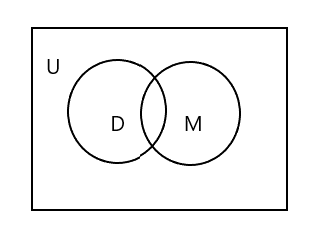
Notarás que en el diagrama de Venn anterior, U representa el área rectangular completa. Los conjuntos D y M están representados por círculos. Los dos círculos se cruzan porque tienen pocos elementos en común. Aquí 'Tim' es un elemento común en ambos conjuntos.
La Intersección de conjuntos representa elementos que son comunes en ambos conjuntos y se denota con el símbolo ' \(\cap\) '.
La porción sombreada en el siguiente diagrama representa \(D \cap M\)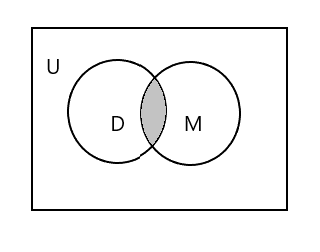
\(D \cap M = \) {Tim}
\(n(D \cap M) = 1\)
Supongamos que queremos enumerar todos los estudiantes que asisten a danza o música o ambos.
La unión de dos conjuntos dados es el conjunto más pequeño que contiene todos los elementos de ambos conjuntos. Se denota por el símbolo 'U'. La porción sombreada en el siguiente diagrama representa \(D \cup M\)
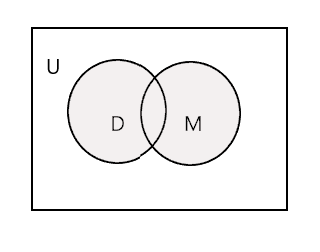
\(D \cup M =\) {Juan, Tim, María, Lee, Fred, Tracy, Danny, Tom}
\(n(D \cup M) = 8\)
También puede restar un conjunto de otro. Aquí D - M representará al conjunto de alumnos que asisten a danza pero no a música.
\(D − M = \) { Juan, María, Lee }
\(n(D - M) = 3\)
La porción sombreada en el siguiente diagrama de Venn representa D - M:
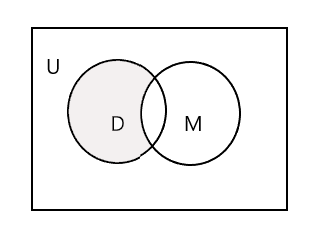
Tomemos el tercer grupo, un grupo de estudiantes que asisten a clases de pintura. P = {Juan, Sam, Danny, Tracy} y n(P) = 4
Diagrama de Venn para representar los tres conjuntos:
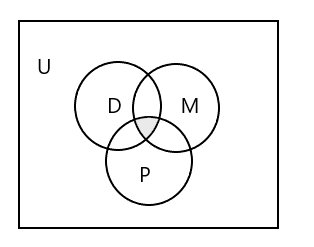
¿Cómo representar el conjunto de estudiantes que asiste a las tres clases?
Respuesta: \(D \cap M \cap P\) = { }, ya que ningún estudiante asiste a las tres clases. Mira la parte sombreada en el diagrama de Venn anterior.
¿Cómo representar al conjunto de alumnos que asisten a clases de danza y pintura?
Responder:
\(D \cap P =\) {Juan}
\(n(D \cap P) = 1\)