Tu vas apprendre:
Un diagramme de Venn est un diagramme qui montre la relation entre et parmi des ensembles qui partagent quelque chose en commun. Ces diagrammes représentent des éléments sous forme de points dans un plan et des ensembles sous forme de régions à l'intérieur de la courbe fermée (généralement un cercle).
Le diagramme de Venn est une manière schématique de représenter les éléments d'un ensemble ou d'un groupe. Maintenant, comme nous l'avons déjà appris ensemble et ses propriétés. Essayons de présenter des ensembles en utilisant le diagramme de Venn.
Exemple : Il y a 10 élèves dans une classe. Certains élèves se sont inscrits à des cours parascolaires comme la peinture, la natation, la musique et la danse.
Ici, l'ensemble universel représente les élèves de la classe. L'ensemble universel est un ensemble contenant tous les objets ou éléments et dont les autres ensembles sont des sous-ensembles.
U = {John, Sam, Lee, Mary, Fred, Danny, Tom, Venn, Tim, Tracy}
L'ensemble d'étudiants assistant au cours de danse est D = {John, Tim, Mary, Lee} ; Le nombre d'éléments dans l'ensemble D est 4, \(n(D) = 4\)
L'ensemble d'étudiants qui suivent un cours de musique est M = {Fred, Tracy, Tim, Danny, Tom} ; Le nombre d'éléments dans l'ensemble M est 5, \(n(M) = 5\)
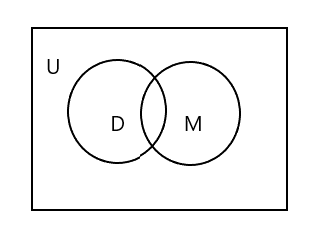
Vous remarquerez que dans le diagramme de Venn ci-dessus, U représente l'ensemble de la zone rectangulaire. Les ensembles D et M sont représentés par des cercles. Les deux cercles se croisent car ils ont peu d'éléments en commun. Ici, "Tim" est un élément commun aux deux ensembles.
L' intersection d'ensembles représente les éléments communs aux deux ensembles et est désignée par le symbole ' \(\cap\) '.
La partie ombrée dans le diagramme ci-dessous représente \(D \cap M\)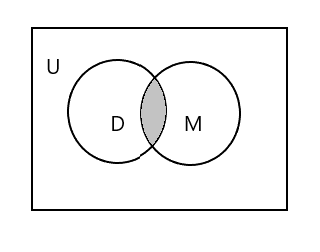
\(D \cap M = \) {Tim}
\(n(D \cap M) = 1\)
Supposons que nous souhaitions répertorier tous les étudiants qui fréquentent soit la danse, soit la musique, soit les deux.
L' union de deux ensembles donnés est le plus petit ensemble qui contient tous les éléments des deux ensembles. Il est désigné par le symbole 'U'. La partie ombrée dans le diagramme ci-dessous représente \(D \cup M\)
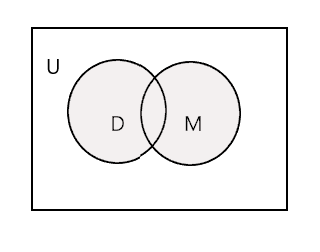
\(D \cup M =\) {John, Tim, Mary, Lee, Fred, Tracy, Danny, Tom}
\(n(D \cup M) = 8\)
Vous pouvez également soustraire un ensemble d'un autre. Ici , D - M représentera l'ensemble des étudiants qui fréquentent la danse mais pas la musique.
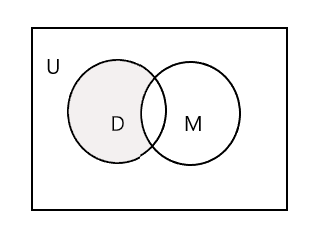
\(D − M = \) { Jean, Marie, Lee }
\(n(D - M) = 3\)
La partie ombrée dans le diagramme de Venn ci-dessous représente D - M :
Prenons le troisième groupe, un groupe d'étudiants qui suivent un cours de peinture. P = {John, Sam, Danny, Tracy} et n(P) = 4
Diagramme de Venn pour représenter les trois ensembles :
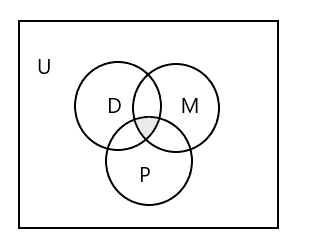
Comment représenter l'ensemble des élèves qui fréquentent les trois classes ?
Réponse : \(D \cap M \cap P\) = { }, car aucun élève n'assiste aux trois cours. Regardez la partie ombrée dans le diagramme de Venn ci-dessus.
Comment représenter l'ensemble des élèves qui fréquentent les cours de danse et de peinture ?
Réponse:
\(D \cap P =\) {Jean}
\(n(D \cap P) = 1\)