Naučit ćeš:
Vennov dijagram je dijagram koji pokazuje odnos između i između skupova koji imaju nešto zajedničko. Ovi dijagrami prikazuju elemente kao točke u ravnini i skupove kao regije unutar zatvorene krivulje (obično kružnice).
Vennov dijagram je shematski način predstavljanja elemenata skupa ili grupe. Sada kao što smo već naučili skup i njegova svojstva. Pokušajmo predstaviti skupove koristeći Vennov dijagram.
Primjer: U razredu ima 10 učenika. Neki učenici su se sami upisali u izvannastavnu nastavu poput slikanja, plivanja, glazbe i plesa.
Ovdje Univerzalni skup predstavlja učenike razreda. Univerzalni skup je skup koji sadrži sve objekte ili elemente i čiji su drugi skupovi podskupovi.
U = {John, Sam, Lee, Mary, Fred, Danny, Tom, Venn, Tim, Tracy}
Skup učenika koji pohađaju sat plesa je D = {John, Tim, Mary, Lee} ; Broj elementa u skupu D je 4, \(n(D) = 4\)
Skup učenika koji pohađaju sat glazbe je M = {Fred, Tracy, Tim, Danny, Tom} ; Broj elementa u skupu M je 5, \(n(M) = 5\)
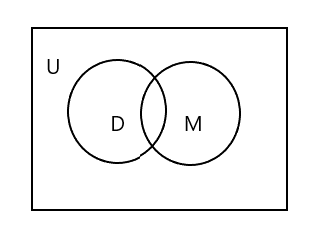
Primijetit ćete da u gornjem Vennovom dijagramu U predstavlja cijelo pravokutno područje. D i M skup su predstavljeni kružnicama. Dva kruga se sijeku jer imaju malo zajedničkih elemenata. Ovdje je 'Tim' zajednički element u oba seta.
Presjek skupova predstavlja elemente koji su zajednički u oba skupa i označen je simbolom ' \(\cap\) '.
Zasjenjeni dio na donjem dijagramu predstavlja \(D \cap M\)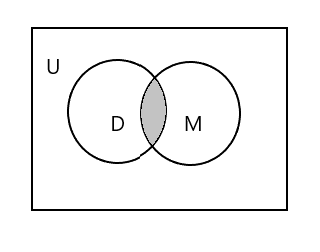
\(D \cap M = \) {Tim}
\(n(D \cap M) = 1\)
Pretpostavimo da želimo navesti sve učenike koji pohađaju ples ili glazbu ili oboje.
Unija dva zadana skupa je najmanji skup koji sadrži sve elemente oba skupa. Označava se simbolom 'U'. Zasjenjeni dio na donjem dijagramu predstavlja \(D \cup M\)
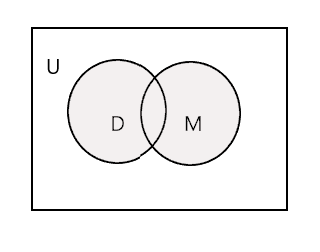
\(D \cup M =\) {John, Tim, Mary, Lee, Fred, Tracy, Danny, Tom}
\(n(D \cup M) = 8\)
Također možete oduzeti jedan skup od drugog. Ovdje će D - M predstavljati skup učenika koji pohađaju ples, ali ne i glazbu.
\(D − M = \) { John, Mary, Lee }
\(n(D - M) = 3\)
Zasjenjeni dio na donjem Vennovom dijagramu predstavlja D - M:
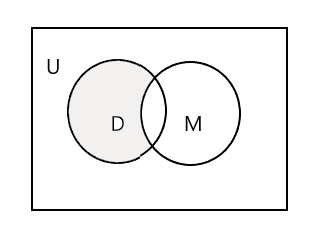
Uzmimo treći set, skup učenika koji pohađaju sat slikanja. P = {John, Sam, Danny, Tracy} i n(P) = 4
Vennov dijagram za predstavljanje sva tri skupa:
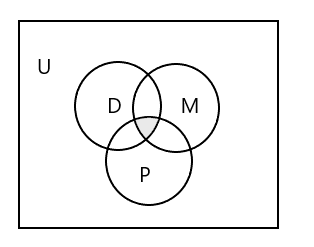
Kako predstaviti skup učenika koji pohađa sva tri razreda?
Odgovor: \(D \cap M \cap P\) = { }, jer nijedan učenik ne pohađa sva tri razreda. Pogledajte zasjenjeni dio na gornjem Vennovom dijagramu.
Kako predstaviti skup učenika koji pohađa sat plesa i slikanja?
Odgovor:
\(D \cap P =\) {John}
\(n(D \cap P) = 1\)