Anda akan belajar:
Diagram Venn adalah diagram yang menunjukkan hubungan antara dan di antara himpunan yang memiliki kesamaan. Diagram ini menggambarkan elemen sebagai titik pada bidang dan ditetapkan sebagai daerah di dalam kurva tertutup (biasanya lingkaran).
Diagram Venn adalah cara skematik untuk merepresentasikan elemen-elemen dari suatu himpunan atau grup. Sekarang seperti yang sudah kita pelajari set dan propertinya. Mari kita coba menyajikan himpunan dengan diagram Venn.
Contoh: Dalam satu kelas terdapat 10 siswa. Beberapa siswa telah mendaftarkan diri di kelas ekstrakurikuler seperti melukis, berenang, musik dan menari.
Di sini set Universal mewakili siswa kelas. Himpunan Universal adalah himpunan yang berisi semua objek atau elemen dan himpunan lainnya adalah subhimpunan.
U = {John, Sam, Lee, Mary, Fred, Danny, Tom, Venn, Tim, Tracy}
Himpunan siswa yang mengikuti kelas tari adalah D = {John, Tim, Mary, Lee} ; Jumlah elemen pada himpunan D adalah 4, \(n(D) = 4\)
Himpunan siswa yang mengikuti kelas musik adalah M = {Fred, Tracy, Tim, Danny, Tom} ; Jumlah elemen dalam himpunan M adalah 5, \(n(M) = 5\)
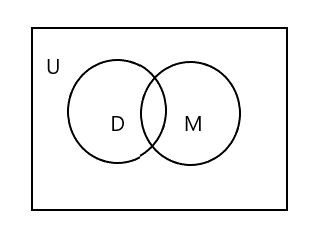
Anda akan melihat bahwa dalam diagram Venn di atas U mewakili seluruh luas persegi panjang. Himpunan D dan M dilambangkan dengan lingkaran. Kedua lingkaran berpotongan karena mereka memiliki beberapa elemen yang sama. Di sini 'Tim' adalah elemen umum di kedua himpunan.
Persimpangan himpunan mewakili elemen yang sama di kedua himpunan dan dilambangkan dengan simbol ' \(\cap\) '.
Bagian yang diarsir pada diagram di bawah menunjukkan \(D \cap M\)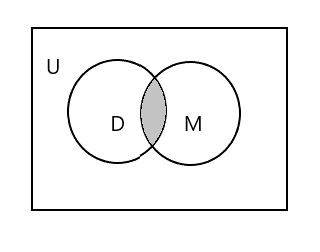
\(D \cap M = \) {Tim}
\(n(D \cap M) = 1\)
Misalkan kita ingin membuat daftar semua siswa yang menghadiri tarian atau musik atau keduanya.
Penyatuan dua himpunan adalah himpunan terkecil yang memuat semua elemen dari kedua himpunan tersebut. Itu dilambangkan dengan simbol 'U'. Bagian yang diarsir pada diagram di bawah menunjukkan \(D \cup M\)
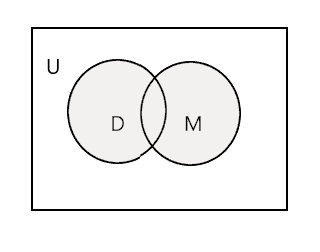
\(D \cup M =\) {John, Tim, Mary, Lee, Fred, Tracy, Danny, Tom}
\(n(D \cup M) = 8\)
Anda juga dapat mengurangi satu set dari yang lain. Di sini D - M akan mewakili kumpulan siswa yang menghadiri tarian tetapi bukan musik.
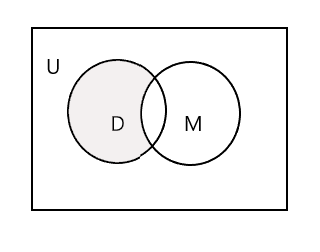
\(D − M = \) { John, Mary, Lee }
\(n(D - M) = 3\)
Bagian yang diarsir pada diagram Venn di bawah ini menyatakan D - M :
Mari kita ambil set ketiga, set siswa yang menghadiri kelas melukis. P = {John, Sam, Danny, Tracy} dan n(P) = 4
Diagram Venn untuk mewakili ketiga himpunan:
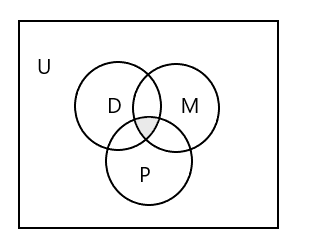
Bagaimana cara mewakili kumpulan siswa yang menghadiri ketiga kelas?
Jawaban: \(D \cap M \cap P\) = { }, karena tidak ada siswa yang mengikuti ketiga kelas tersebut. Perhatikan bagian yang diarsir pada diagram Venn di atas.
Bagaimana merepresentasikan himpunan siswa yang mengikuti kelas tari dan lukis?
Menjawab:
\(D \cap P =\) {John}
\(n(D \cap P) = 1\)