Imparerai:
Un diagramma di Venn è un diagramma che mostra la relazione tra e tra insiemi che condividono qualcosa in comune. Questi diagrammi rappresentano gli elementi come punti su un piano e gli insiemi come regioni all'interno della curva chiusa (di solito un cerchio).
Il diagramma di Venn è un modo schematico di rappresentare gli elementi di un insieme o di un gruppo. Ora come abbiamo già imparato insieme e le sue proprietà. Proviamo a presentare gli insiemi usando il diagramma di Venn.
Esempio: Ci sono 10 studenti in una classe. Alcuni studenti si sono iscritti a corsi extrascolastici come pittura, nuoto, musica e danza.
Qui il set universale rappresenta gli studenti della classe. L'insieme universale è un insieme contenente tutti gli oggetti o elementi e di cui altri insiemi sono sottoinsiemi.
U = {John, Sam, Lee, Mary, Fred, Danny, Tom, Venn, Tim, Tracy}
L'insieme degli studenti che frequentano il corso di danza è D = {John, Tim, Mary, Lee} ; Il numero di elementi nell'insieme D è 4, \(n(D) = 4\)
L'insieme degli studenti che frequentano il corso di musica è M = {Fred, Tracy, Tim, Danny, Tom} ; Il numero di elementi nell'insieme M è 5, \(n(M) = 5\)
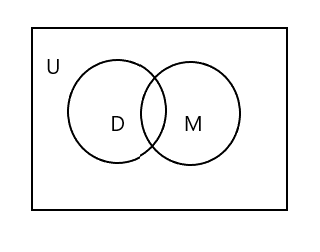
Noterai che nel diagramma di Venn sopra U rappresenta l'intera area rettangolare. Gli insiemi D e M sono rappresentati da cerchi. I due cerchi si intersecano perché hanno pochi elementi in comune. Qui 'Tim' è un elemento comune in entrambi i set.
L' intersezione degli insiemi rappresenta gli elementi comuni in entrambi gli insiemi ed è indicata dal simbolo ' \(\cap\) '.
La parte ombreggiata nel diagramma sottostante rappresenta \(D \cap M\)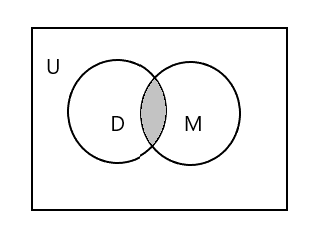
\(D \cap M = \) {Tim}
\(n(D \cap M) = 1\)
Supponiamo di voler elencare tutti gli studenti che frequentano danza o musica o entrambi.
L' unione di due insiemi dati è l'insieme più piccolo che contiene tutti gli elementi di entrambi gli insiemi. È indicato dal simbolo 'U'. La parte ombreggiata nel diagramma sottostante rappresenta \(D \cup M\)
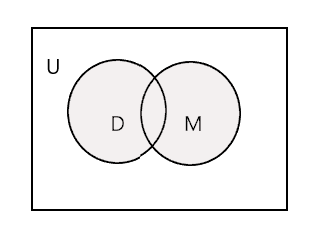
\(D \cup M =\) {John, Tim, Mary, Lee, Fred, Tracy, Danny, Tom}
\(n(D \cup M) = 8\)
Puoi anche sottrarre un insieme da un altro. Qui D - M rappresenterà l'insieme degli studenti che frequentano la danza ma non la musica.
\(D − M = \) { Giovanni, Maria, Lee }
\(n(D - M) = 3\)
La parte ombreggiata nel diagramma di Venn sottostante rappresenta D - M :
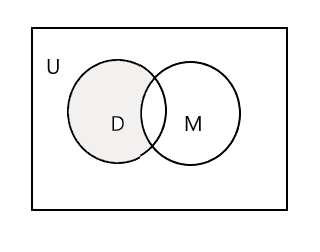
Prendiamo il terzo set, un gruppo di studenti che frequentano il corso di pittura. P = {John, Sam, Danny, Tracy} e n(P) = 4
Diagramma di Venn per rappresentare tutti e tre gli insiemi:
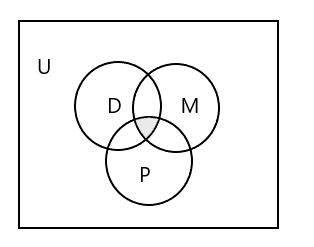
Come rappresentare l'insieme degli studenti che frequentano tutte e tre le classi?
Risposta: \(D \cap M \cap P\) = { }, in quanto nessuno studente frequenta tutte e tre le classi. Guarda la parte ombreggiata nel diagramma di Venn sopra.
Come rappresentare l'insieme degli studenti che frequentano il corso di danza e pittura?
Risposta:
\(D \cap P =\) {Giovanni}
\(n(D \cap P) = 1\)