学習内容:
ベン図は、共通点のあるセット間の関係を示す図です。これらのダイアグラムは、エレメントを平面内のポイントとして表し、セットを閉じた曲線 (通常は円) 内の領域として表します。
ベン図は、セットまたはグループの要素を表す概略的な方法です。セットとそのプロパティについてはすでに学習しました。ベン図を使って集合を表現してみましょう。
例: 1 クラスに 10 人の生徒がいます。一部の学生は、絵画、水泳、音楽、ダンスなどの課外クラスに登録しています。
ここで、ユニバーサル セットはクラスの生徒を表します。ユニバーサル セットは、すべてのオブジェクトまたは要素を含むセットであり、他のセットはそのサブセットです。
U = {ジョン、サム、リー、メアリー、フレッド、ダニー、トム、ベン、ティム、トレーシー}
ダンスクラスに参加している生徒の集合は D = {ジョン、ティム、メアリー、リー} です。セット D の要素数は 4、 \(n(D) = 4\)
音楽の授業に参加している生徒の集合は M = {Fred, Tracy, Tim, Danny, Tom} です。セット M の要素数は 5、 \(n(M) = 5\)
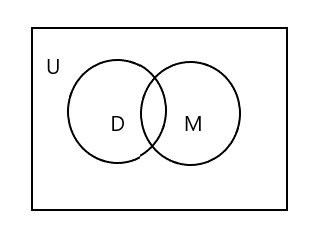
上記のベン図では、U が長方形の領域全体を表していることがわかります。 D と M セットは丸で表されます。 2 つの円は、共通する要素がほとんどないため、交差しています。ここで、'Tim' は両方のセットに共通の要素です。
集合の交差は、両方の集合に共通する要素を表し、記号 ' \(\cap\) ' で示されます。
下図の網掛け部分は\(D \cap M\)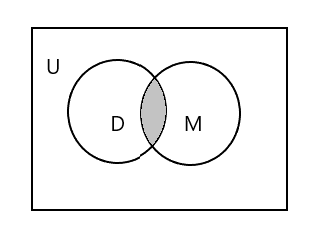
\(D \cap M = \) {ティム}
\(n(D \cap M) = 1\)
ダンスか音楽、またはその両方に参加しているすべての生徒をリストしたいとします。
与えられた 2 つの集合の和集合は、両方の集合のすべての要素を含む最小の集合です。記号「U」で表されます。下図の網掛け部分が\(D \cup M\)
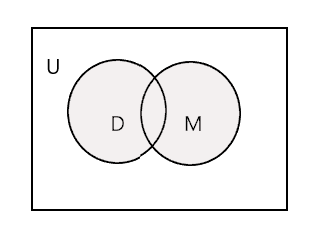
\(D \cup M =\) {ジョン、ティム、メアリー、リー、フレッド、トレーシー、ダニー、トム}
\(n(D \cup M) = 8\)
あるセットから別のセットを差し引くこともできます。ここで、 D - M は、ダンスには参加するが音楽には参加しない生徒のセットを表します。
\(D − M = \) { ジョン、メアリー、リー }
\(n(D - M) = 3\)
以下のベン図の網掛け部分は D - M を表します。
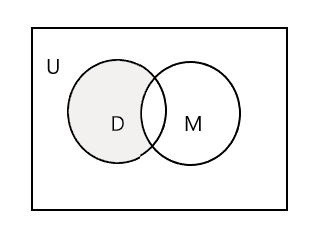
3 番目のセットは、絵画のクラスに参加する生徒のセットです。 P = {ジョン、サム、ダニー、トレーシー} および n(P) = 4
3 つのセットすべてを表すベン図:
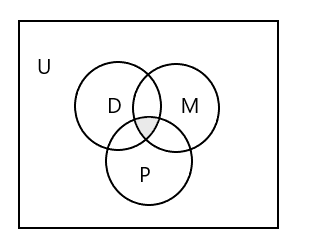
3 つのクラスすべてに出席する生徒の集合を表す方法は?
答え: \(D \cap M \cap P\) = { }。3 つのクラスすべてに出席する生徒はいないからです。上のベン図の網掛け部分を見てください。
ダンスと絵画のクラスに参加する生徒のセットをどのように表現しますか?
答え:
\(D \cap P =\) {ジョン}
\(n(D \cap P) = 1\)