Ти ќе научиш:
Венов дијаграм е дијаграм што ја прикажува врската помеѓу и меѓу множествата што споделуваат нешто заедничко. Овие дијаграми прикажуваат елементи како точки во рамнината и се поставуваат како региони во затворената крива (обично круг).
Венов дијаграм е шематски начин на претставување на елементите на множество или група. Сега како што веќе научивме множество и неговите својства. Ајде да се обидеме да претставиме множества користејќи Венов дијаграм.
Пример: Во паралелката има 10 ученици. Некои ученици се запишале на воннаставни часови како сликање, пливање, музика и танц.
Овде Универзалниот сет ги претставува учениците од класот. Универзалното множество е множество што ги содржи сите објекти или елементи и чии подмножества се другите множества.
U = {Џон, Сем, Ли, Мери, Фред, Дени, Том, Вен, Тим, Трејси}
Збир на ученици кои посетуваат час по танц е D = {Џон, Тим, Мери, Ли} ; Број на елемент во множеството D е 4, \(n(D) = 4\)
Збир на ученици кои посетуваат часови по музика е М = {Фред, Трејси, Тим, Дени, Том} ; Број на елемент во множеството М е 5, \(n(M) = 5\)
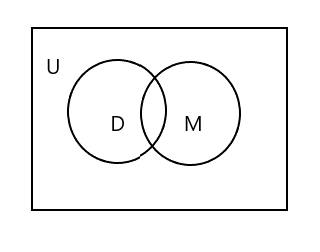
Ќе забележите дека на горниот Венов дијаграм U ја претставува целата правоаголна површина. D и M множеството се претставени со кругови. Двата круга се вкрстуваат бидејќи имаат малку заеднички елементи. Овде „Тим“ е заеднички елемент и во двата сета.
Пресекот на множества претставува елементи кои се заеднички во двете множества и се означува со симболот ' \(\cap\) '.
Засенчениот дел на дијаграмот подолу претставува \(D \cap M\)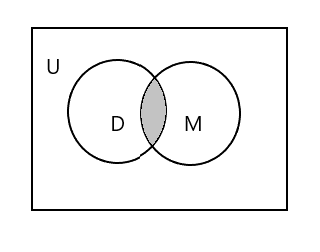
\(D \cap M = \) {Тим}
\(n(D \cap M) = 1\)
Да претпоставиме дека сакаме да ги наведеме сите студенти кои посетуваат танц или музика или и двете.
Унија на две дадени множества е најмалото множество кое ги содржи сите елементи на двете множества. Се означува со симболот „U“. Засенчениот дел на дијаграмот подолу претставува \(D \cup M\)
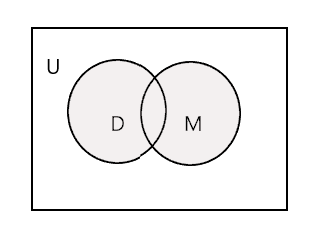
\(D \cup M =\) {Џон, Тим, Мери, Ли, Фред, Трејси, Дени, Том}
\(n(D \cup M) = 8\)
Можете исто така да одземете едно множество од друго. Овде D - M ќе го претставува множеството студенти кои посетуваат танц, но не и музика.
\(D − M = \) { Џон, Мери, Ли }
\(n(D - M) = 3\)
Засенчениот дел во долунаведениот Венов дијаграм го претставува D - M:
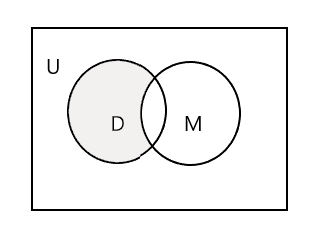
Да го земеме третиот сет, збир на ученици кои посетуваат час по сликарство. P = {Џон, Сем, Дени, Трејси} и n(P) = 4
Венов дијаграм за претставување на сите три множества:
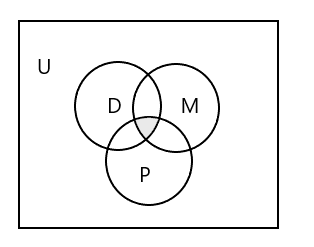
Како да се претстави множеството ученици кои ги посетуваат сите три паралелки?
Одговор: \(D \cap M \cap P\) = { }, бидејќи ниту еден ученик не ги посетува сите три часови. Погледнете го засенчениот дел во горниот Венов дијаграм.
Како да се претстави множеството ученици кои посетуваат часови по танц и сликање?
Одговор:
\(D \cap P =\) {Џон}
\(n(D \cap P) = 1\)