Та сурах болно:
Венн диаграм нь нийтлэг зүйлийг хуваалцдаг олонлогуудын хоорондын болон хоорондын хамаарлыг харуулсан диаграмм юм. Эдгээр диаграммууд нь элементүүдийг хавтгайн цэг болгон дүрсэлж, хаалттай муруй доторх мужуудыг (ихэвчлэн тойрог) тогтоодог.
Венн диаграм нь олонлог эсвэл бүлгийн элементүүдийг дүрслэх схемийн арга юм. Одоо бид олонлог болон түүний шинж чанаруудыг аль хэдийн сурсан. Венн диаграммыг ашиглан багцуудыг танилцуулахыг хичээцгээе.
Жишээ: Нэг ангид 10 сурагч байна. Зарим оюутнууд уран зураг, усанд сэлэх, хөгжим, бүжиг гэх мэт хичээлээс гадуурх ангид бүртгүүлсэн байна.
Энд Universal багц нь ангийн сурагчдыг төлөөлдөг. Universal олонлог нь бүх объект эсвэл элементүүдийг агуулсан олонлог бөгөөд бусад олонлогууд нь дэд олонлогууд юм.
U = {Жон, Сэм, Ли, Мэри, Фред, Дэнни, Том, Венн, Тим, Трейси}
Бүжгийн хичээлд сууж буй оюутнуудын багц нь D = {Жон, Тим, Мэри, Ли}; D олонлогийн элементийн тоо 4, \(n(D) = 4\)
Хөгжмийн хичээлд сууж буй оюутнуудын багц нь М = {Фред, Трейси, Тим, Данни, Том}; M багц дахь элементийн тоо 5, \(n(M) = 5\)
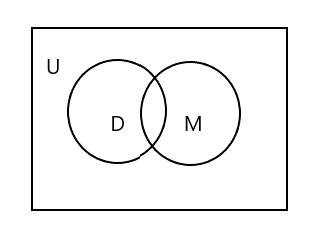
Дээрх Венн диаграммд U нь тэгш өнцөгт талбайг бүхэлд нь төлөөлж байгааг та анзаарах болно. D ба M олонлогийг тойрог хэлбэрээр дүрсэлсэн. Цөөн нийтлэг элементтэй тул хоёр тойрог огтлолцож байна. Энд "Тим" нь хоёр багц дахь нийтлэг элемент юм.
Олонлогуудын огтлолцол нь хоёр олонлогт нийтлэг байдаг элементүүдийг илэрхийлдэг бөгөөд ' \(\cap\) ' тэмдгээр тэмдэглэгдсэн байдаг.
Доорх диаграммд сүүдэрлэсэн хэсэг нь \(D \cap M\) -г илэрхийлнэ.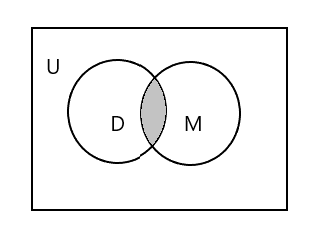
\(D \cap M = \) {Тим}
\(n(D \cap M) = 1\)
Бид бүжиг, хөгжим эсвэл хоёуланд нь оролцдог бүх оюутнуудыг жагсаахыг хүсч байна гэж бодъё.
Өгөгдсөн хоёр олонлогийн нэгдэл нь хоёр олонлогийн бүх элементүүдийг агуулсан хамгийн жижиг олонлог юм. Үүнийг 'U' тэмдгээр тэмдэглэв. Доорх диаграммд сүүдэрлэсэн хэсэг нь \(D \cup M\) -г илэрхийлнэ.
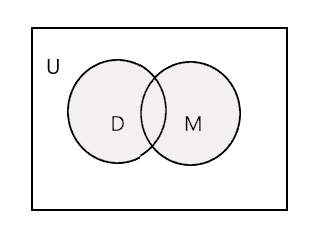
\(D \cup M =\) {Жон, Тим, Мэри, Ли, Фред, Трейси, Дэнни, Том}
\(n(D \cup M) = 8\)
Та мөн нэг багцаас нөгөө багцаас хасаж болно. Энд D - M нь хөгжим биш харин бүжигт оролцдог оюутнуудын багцыг төлөөлөх болно.
\(D − M = \) { Жон, Мэри, Ли }
\(n(D - M) = 3\)
Доорх Венн диаграмм дахь сүүдэртэй хэсэг нь D - M -г илэрхийлнэ.
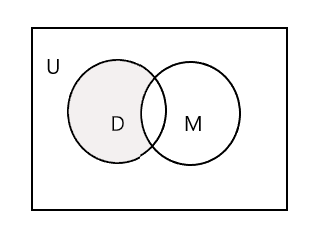
Гурав дахь багц буюу зургийн хичээлд суудаг оюутнуудын багцыг авцгаая. P = {Жон, Сэм, Дэнни, Трейси} ба n (P) = 4
Гурван багцыг төлөөлөх Венн диаграм:
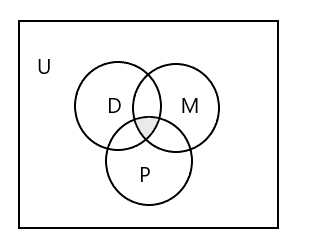
Гурван ангид хамрагддаг оюутнуудын багцыг хэрхэн төлөөлөх вэ?
Хариулт: \(D \cap M \cap P\) = { }, учир нь гурван ангид нэг ч сурагч хамрагдахгүй. Дээрх Венн диаграмын сүүдэртэй хэсгийг хар.
Бүжиг, уран зургийн хичээлд хамрагддаг оюутнуудын багцыг хэрхэн төлөөлөх вэ?
Хариулт:
\(D \cap P =\) {Жон}
\(n(D \cap P) = 1\)