သင်ယူရလိမ့်မည်-
Venn diagram သည် တူညီသောအရာတစ်ခုကို မျှဝေသည့် set များကြားနှင့် အကြား ဆက်နွယ်မှုကို ပြသသည့် diagram တစ်ခုဖြစ်သည်။ ဤပုံချပ်များသည် လေယာဉ်တစ်ခုရှိ အမှတ်များအဖြစ် အစိတ်အပိုင်းများကို သရုပ်ဖော်ပြီး အပိတ်မျဉ်းအတွင်း (များသောအားဖြင့် စက်ဝိုင်းတစ်ခု) အဖြစ် သတ်မှတ်သည်။
Venn diagram သည် set သို့မဟုတ် group တစ်ခု၏ element များကိုကိုယ်စားပြုသည့် schematic နည်းလမ်းတစ်ခုဖြစ်သည်။ ယခု ကျွန်ုပ်တို့ လေ့လာထားပြီးဖြစ်သည့်အတိုင်း Set နှင့် ၎င်း၏ ဂုဏ်သတ္တိများ။ Venn diagram ကို အသုံးပြု၍ အစုံများကို တင်ပြကြည့်ရအောင်။
ဥပမာ- အတန်းတစ်ခုတွင် ကျောင်းသား ၁၀ ယောက်ရှိသည်။ အချို့သော ကျောင်းသားများသည် ပန်းချီ၊ ရေကူး၊ တေးဂီတနှင့် အကများကဲ့သို့ သင်ရိုးညွှန်းတမ်း ပြင်ပသင်တန်းများတွင် စာရင်းသွင်းထားကြသည်။
ဤနေရာတွင် Universal set သည် အတန်း၏ကျောင်းသားများကို ကိုယ်စားပြုသည်။ Universal set သည် အရာဝတ္တုများ သို့မဟုတ် ဒြပ်စင်များပါ၀င်သော အစုတစ်ခုဖြစ်ပြီး ၎င်းအနက်မှ အခြားအစုများသည် အစုခွဲများဖြစ်သည်။
U = {John, Sam, Lee, Mary, Fred, Danny, Tom, Venn, Tim, Tracy}
အကသင်တန်းတက်သည့် ကျောင်းသားများ၏ အစုံမှာ D = {John, Tim, Mary, Lee} ; Set D တွင် ပါဝင်သည့် အစိတ်အပိုင်းအရေအတွက်သည် 4 ဖြစ်ပြီး \(n(D) = 4\)
ဂီတသင်တန်းတက်ရောက်နေသည့် ကျောင်းသားများ၏ အစုမှာ M = {Fred၊ Tracy၊ Tim, Danny, Tom} ; Set M တွင် ဒြပ်စင်အရေအတွက်သည် 5 ဖြစ်ပြီး \(n(M) = 5\)
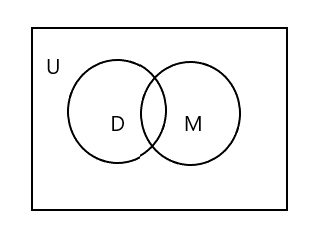
အထက်ဖော်ပြပါ Venn ပုံတွင် U သည် စတုဂံဧရိယာတစ်ခုလုံးကို ကိုယ်စားပြုကြောင်း သင်သတိပြုမိပါလိမ့်မည်။ D နှင့် M set ကို စက်ဝိုင်းများဖြင့် ကိုယ်စားပြုသည်။ စက်ဝိုင်းနှစ်ခုသည် တူညီသောဒြပ်စင်အနည်းငယ်ပါရှိသောကြောင့် စက်ဝိုင်းနှစ်ခုသည် ဖြတ်တောက်နေသည်။ ဤတွင် 'Tim' သည် အစုံနှစ်ခုစလုံးတွင် ဘုံဒြပ်စင်တစ်ခုဖြစ်သည်။
sets ၏ ဖြတ်ပိုင်းသည် set နှစ်ခုစလုံးတွင် အသုံးများသော element များကို ကိုယ်စားပြုပြီး ' \(\cap\) ' သင်္ကေတဖြင့် ဖော်ပြသည်။
အောက်ဖော်ပြပါ ပုံတွင် ပြထားသော အပိုင်းသည် \(D \cap M\) ကို ကိုယ်စားပြုသည်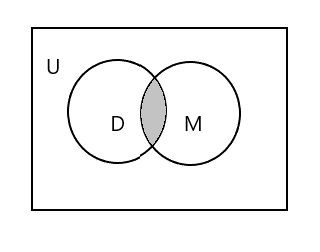
\(D \cap M = \) { Tim }
\(n(D \cap M) = 1\)
အက သို့မဟုတ် ဂီတ သို့မဟုတ် နှစ်ခုလုံးတက်ရောက်သော ကျောင်းသားအားလုံးကို စာရင်းပြုစုလိုသည်ဆိုပါစို့။
ပေးထားသော အတွဲနှစ်ခု၏ သမဂ္ဂ သည် အတွဲနှစ်ခုစလုံး၏ အစိတ်အပိုင်းအားလုံးပါရှိသော အသေးငယ်ဆုံးအတွဲဖြစ်သည်။ ၎င်းကို 'U' သင်္ကေတဖြင့် ရည်ညွှန်းသည်။ အောက်ဖော်ပြပါပုံတွင် အရိပ်ပြထားသောအပိုင်းသည် \(D \cup M\) ကို ကိုယ်စားပြုသည်
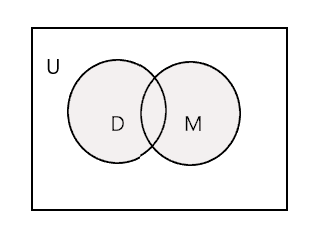
\(D \cup M =\) {John၊ Tim၊ Mary၊ Lee၊ Fred၊ Tracy၊ Danny၊ Tom}
\(n(D \cup M) = 8\)
အစုတစ်ခုမှ အခြားတစ်ခုကိုလည်း နုတ် နိုင်သည်။ ဤနေရာတွင် D-M သည် အကတက်သော်လည်း ဂီတ မဟုတ်သော ကျောင်းသားများကို ကိုယ်စားပြုသည်။
\(D − M = \) { ဂျွန်၊ မေရီ၊ လီ }
\(n(D - M) = 3\)
အောက်ဖော်ပြပါ Venn ပုံတွင် အရိပ်ပြထားသောအပိုင်းသည် D - M ကို ကိုယ်စားပြုသည်။
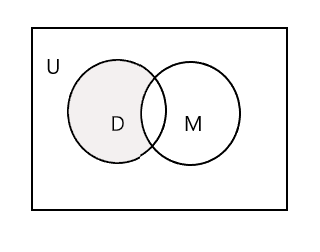
တတိယအတွဲ၊ ပန်းချီသင်တန်းတက်နေတဲ့ ကျောင်းသားတွေ အစုံလိုက်ကြရအောင်။ P = {John, Sam, Danny, Tracy} နှင့် n(P) = 4
သုံးစုံလုံးကို ကိုယ်စားပြုရန် Venn diagram
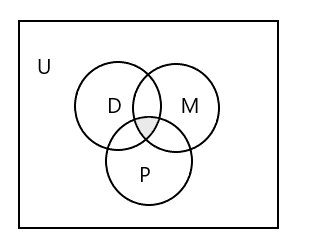
အတန်း (၃) တန်းစလုံးတက်တဲ့ ကျောင်းသားတွေကို ဘယ်လိုကိုယ်စားပြုမလဲ။
အဖြေ- \(D \cap M \cap P\) = { } ၊ မည်သည့်ကျောင်းသားမှ အတန်းသုံးတန်းလုံးကို မတက်နိုင်ပါ။ အပေါ်က Venn ပုံမှာ ပြထားတဲ့ အပိုင်းကို ကြည့်ပါ။
အကနဲ့ ပန်းချီသင်တန်းတက်တဲ့ ကျောင်းသားတွေကို ဘယ်လိုကိုယ်စားပြုမလဲ။
အဖြေ-
\(D \cap P =\) {ယောဟန်}
\(n(D \cap P) = 1\)