तपाईंले सिक्नुहुनेछ:
भेन रेखाचित्र एक रेखाचित्र हो जसले सेटहरू बीचको सम्बन्धलाई देखाउँदछ जुन साझामा केहि साझा गर्दछ। यी रेखाचित्रहरूले तत्वहरूलाई विमानमा बिन्दुहरूको रूपमा चित्रण गर्दछ र बन्द वक्र भित्र क्षेत्रहरूको रूपमा सेट गर्दछ (सामान्यतया एउटा सर्कल)।
Venn रेखाचित्र सेट वा समूह को तत्वहरु को प्रतिनिधित्व को एक योजनाबद्ध तरीका हो। अब हामीले पहिले नै सेट र यसको गुणहरू सिकेका छौं। भेन रेखाचित्र प्रयोग गरेर सेटहरू प्रस्तुत गर्ने प्रयास गरौं।
उदाहरण: एउटा कक्षामा १० जना विद्यार्थी छन्। केही विद्यार्थीहरूले चित्रकला, पौडी, संगीत र नृत्य जस्ता अतिरिक्त कक्षाहरूमा भर्ना गरेका छन्।
यहाँ विश्वव्यापी सेटले कक्षाका विद्यार्थीहरूलाई प्रतिनिधित्व गर्दछ। युनिभर्सल सेट भनेको सबै वस्तु वा तत्वहरू भएको सेट हो र जसका अन्य सेटहरू सबसेटहरू हुन्।
U = {जोन, सैम, ली, मेरी, फ्रेड, डैनी, टम, भेन, टिम, ट्रेसी}
नृत्य कक्षामा भाग लिने विद्यार्थीहरूको सेट हो D = {John, Tim, Mary, Lee} ; सेट D मा तत्वको संख्या 4 हो, \(n(D) = 4\)
संगीत कक्षामा भाग लिने विद्यार्थीहरूको सेट हो M = {फ्रेड, ट्रेसी, टिम, ड्यानी, टम}; सेट M मा तत्वको संख्या 5 हो, \(n(M) = 5\)
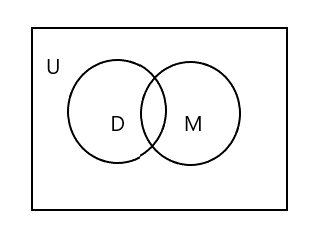
तपाईंले याद गर्नुहुनेछ कि माथिको भेन रेखाचित्रमा U ले सम्पूर्ण आयताकार क्षेत्रलाई प्रतिनिधित्व गरिरहेको छ। D र M सेट सर्कलहरूद्वारा प्रतिनिधित्व गरिन्छ। दुई सर्कलहरू मिल्दोजुल्दो तत्वहरू भएका हुनाले तिनीहरू प्रतिच्छेदन गर्दैछन्। यहाँ 'टिम' दुबै सेटहरूमा साझा तत्व हो।
सेटहरूको प्रतिच्छेदनले तत्वहरूलाई प्रतिनिधित्व गर्दछ जुन दुवै सेटहरूमा सामान्य हुन्छ र ' \(\cap\) ' प्रतीकद्वारा जनाइएको हुन्छ।
तलको रेखाचित्रमा छायांकन गरिएको भागले प्रतिनिधित्व गर्दछ \(D \cap M\)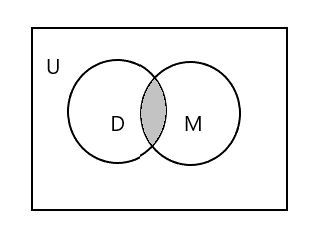
\(D \cap M = \) {टिम}
\(n(D \cap M) = 1\)
मानौं हामी नृत्य वा संगीत वा दुवैमा सहभागी हुने सबै विद्यार्थीहरूलाई सूचीकृत गर्न चाहन्छौं।
दिइएको दुई सेटहरूको संघ सबैभन्दा सानो सेट हो जसमा दुवै सेटका सबै तत्वहरू छन्। यो प्रतीक 'U' द्वारा जनाइएको छ। तलको रेखाचित्रमा छायांकित भागले प्रतिनिधित्व गर्दछ \(D \cup M\)
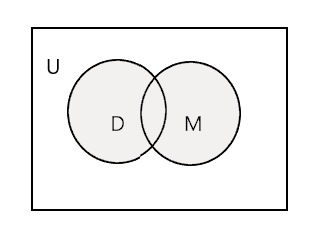
\(D \cup M =\) {जोन, टिम, मेरी, ली, फ्रेड, ट्रेसी, डैनी, टम}
\(n(D \cup M) = 8\)
तपाईले एउटा सेटलाई अर्कोबाट घटाउन पनि सक्नुहुन्छ। यहाँ D - M ले नृत्यमा उपस्थित हुने विद्यार्थीहरूको समूहलाई प्रतिनिधित्व गर्नेछ तर संगीत होइन ।
\(D − M = \) { जोन, मेरी, ली }
\(n(D - M) = 3\)
तलको भेन रेखाचित्रमा छायांकन गरिएको भागले D - M प्रतिनिधित्व गर्दछ:
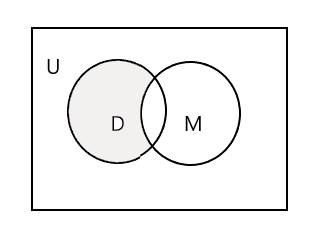
तेस्रो सेट लिनुहोस्, चित्रकला कक्षामा भाग लिने विद्यार्थीहरूको सेट। P = {जोन, सैम, डैनी, ट्रेसी} र n(P) = 4
सबै तीन सेटहरू प्रतिनिधित्व गर्न Venn रेखाचित्र:
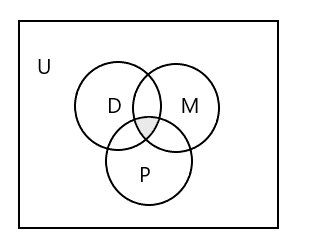
तीनवटै कक्षामा उपस्थित हुने विद्यार्थीहरूको समूहलाई कसरी प्रतिनिधित्व गर्ने?
उत्तर: \(D \cap M \cap P\) = { }, कुनै पनि विद्यार्थी तीनवटै कक्षामा उपस्थित हुँदैनन्। माथिको Venn रेखाचित्रमा छायादार भाग हेर्नुहोस्।
नृत्य र चित्रकला कक्षामा उपस्थित विद्यार्थीहरूको सेट कसरी प्रतिनिधित्व गर्ने?
उत्तर:
\(D \cap P =\) {जोन}
\(n(D \cap P) = 1\)