Je leert:
Een Venn-diagram is een diagram dat de relatie weergeeft tussen en tussen sets die iets gemeen hebben. Deze diagrammen geven elementen weer als punten in een vlak en stellen als gebieden binnen de gesloten curve (meestal een cirkel).
Venn-diagram is een schematische manier om de elementen van een verzameling of groep weer te geven. Nu zoals we al hebben geleerd set en zijn eigenschappen. Laten we proberen sets te presenteren met behulp van het Venn-diagram.
Voorbeeld: Er zitten 10 leerlingen in een klas. Sommige studenten hebben zich ingeschreven voor buitenschoolse lessen zoals schilderen, zwemmen, muziek en dans.
Hier staat Universal set voor studenten van de klas. De universele verzameling is een verzameling die alle objecten of elementen bevat en waarvan andere verzamelingen deelverzamelingen zijn.
U = {John, Sam, Lee, Mary, Fred, Danny, Tom, Venn, Tim, Tracy}
Het aantal studenten dat dansles volgt is D = {John, Tim, Mary, Lee}; Aantal elementen in verzameling D is 4, \(n(D) = 4\)
Het aantal studenten dat muziekles volgt is M = {Fred, Tracy, Tim, Danny, Tom}; Aantal elementen in verzameling M is 5, \(n(M) = 5\)
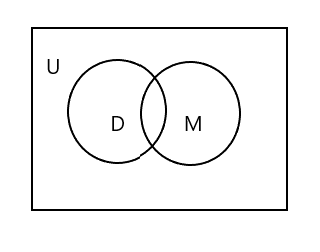
U zult opmerken dat in het bovenstaande Venn-diagram U het hele rechthoekige gebied vertegenwoordigt. D en M set worden weergegeven door cirkels. De twee cirkels kruisen elkaar omdat ze weinig elementen gemeen hebben. Hier is 'Tim' een gemeenschappelijk element in beide sets.
Het snijpunt van verzamelingen vertegenwoordigt elementen die in beide verzamelingen voorkomen en wordt aangeduid met het symbool ' \(\cap\) '.
Het gearceerde gedeelte in het onderstaande diagram staat voor \(D \cap M\)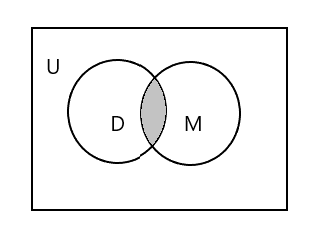
\(D \cap M = \) {Tim}
\(n(D \cap M) = 1\)
Stel dat we alle studenten willen opsommen die ofwel dans ofwel muziek ofwel beide volgen.
Unie van twee gegeven sets is de kleinste set die alle elementen van beide sets bevat. Het wordt aangegeven met het symbool 'U'. Het gearceerde gedeelte in het onderstaande diagram vertegenwoordigt \(D \cup M\)
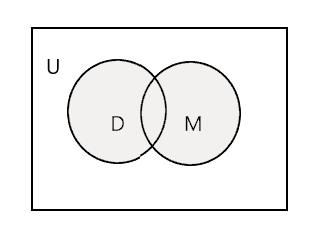
\(D \cup M =\) {John, Tim, Mary, Lee, Fred, Tracy, Danny, Tom}
\(n(D \cup M) = 8\)
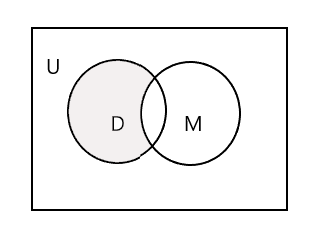
Je kunt ook de ene set van de andere aftrekken . Hier vertegenwoordigt D - M de groep studenten die wel naar dans gaan, maar niet naar muziek.
\(D − M = \) { Jan, Maria, Lee }
\(n(D - M) = 3\)
Het gearceerde gedeelte in het onderstaande Venn-diagram stelt D - M voor:
Laten we de derde set nemen, een groep studenten die schilderlessen volgen. P = {John, Sam, Danny, Tracy} en n(P) = 4
Venn-diagram om alle drie de sets weer te geven:
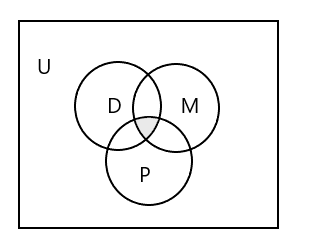
Hoe representeer je de groep studenten die alle drie de lessen bijwoont?
Antwoord: \(D \cap M \cap P\) = { }, aangezien geen enkele leerling alle drie de lessen bijwoont. Kijk naar het gearceerde gedeelte in het bovenstaande Venn-diagram.
Hoe representeer je de groep studenten die naar dans- en schilderlessen gaat?
Antwoorden:
\(D \cap P =\) {Jan}
\(n(D \cap P) = 1\)