Nauczysz się:
Diagram Venna to diagram, który pokazuje relacje między zbiorami i między zbiorami, które mają coś wspólnego. Diagramy te przedstawiają elementy jako punkty na płaszczyźnie, a zbiory jako obszary wewnątrz zamkniętej krzywej (zwykle jest to okrąg).
Diagram Venna to schematyczny sposób przedstawiania elementów zbioru lub grupy. Teraz, jak już poznaliśmy zbiór i jego właściwości. Spróbujmy przedstawić zbiory za pomocą diagramu Venna.
Przykład: W klasie jest 10 uczniów. Niektórzy uczniowie zapisali się na zajęcia pozalekcyjne, takie jak malowanie, pływanie, muzyka i taniec.
Tutaj zestaw uniwersalny reprezentuje uczniów klasy. Zbiór uniwersalny to zbiór zawierający wszystkie obiekty lub elementy, którego podzbiorami są inne zbiory.
U = {John, Sam, Lee, Mary, Fred, Danny, Tom, Venn, Tim, Tracy}
Zbiór uczniów uczęszczających na zajęcia taneczne to D = {John, Tim, Mary, Lee} ; Liczba elementów w zbiorze D wynosi 4, \(n(D) = 4\)
Zbiór uczniów uczęszczających na zajęcia muzyczne to M = {Fred, Tracy, Tim, Danny, Tom} ; Liczba elementów w zbiorze M wynosi 5, \(n(M) = 5\)
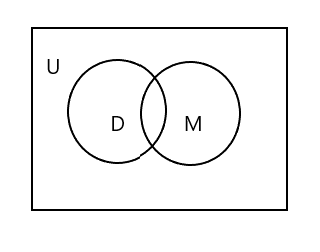
Zauważysz, że na powyższym diagramie Venna U reprezentuje cały prostokątny obszar. Zestawy D i M są reprezentowane przez kółka. Te dwa okręgi przecinają się, ponieważ mają niewiele elementów wspólnych. Tutaj „Tim” jest elementem wspólnym w obu zestawach.
Przecięcie zbiorów reprezentuje elementy, które są wspólne w obu zbiorach i jest oznaczone symbolem ' \(\cap\) '.
Zacieniona część na poniższym diagramie przedstawia \(D \cap M\)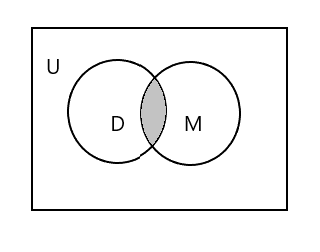
\(D \cap M = \) {Tim}
\(n(D \cap M) = 1\)
Załóżmy, że chcemy wyświetlić listę wszystkich uczniów, którzy uczęszczają na zajęcia taneczne, muzyczne lub jedno i drugie.
Suma dwóch danych zbiorów jest najmniejszym zbiorem, który zawiera wszystkie elementy obu zbiorów. Jest oznaczony symbolem „U”. Zacieniona część na poniższym diagramie przedstawia \(D \cup M\)
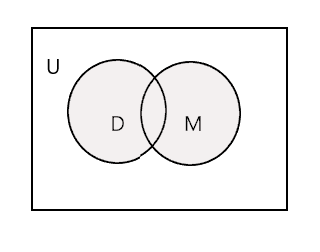
\(D \cup M =\) {John, Tim, Mary, Lee, Fred, Tracy, Danny, Tom}
\(n(D \cup M) = 8\)
Możesz także odjąć jeden zestaw od drugiego. Tutaj D - M będzie reprezentować zbiór uczniów, którzy uczęszczają na taniec, ale nie na muzykę.
\(D − M = \) {Jan, Maria, Lee}
\(n(D - M) = 3\)
Zacieniona część na poniższym diagramie Venna przedstawia D - M:
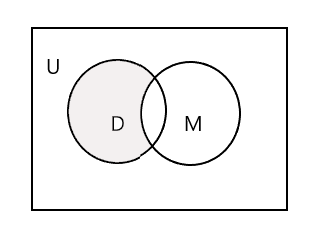
Weźmy trzeci zestaw, grupę uczniów uczęszczających na zajęcia z malarstwa. P = {Jan, Sam, Danny, Tracy} i n(P) = 4
Diagram Venna reprezentujący wszystkie trzy zestawy:
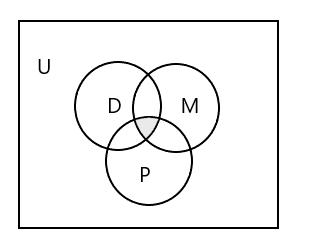
Jak reprezentować zbiór uczniów, którzy uczęszczają na wszystkie trzy zajęcia?
Odpowiedź: \(D \cap M \cap P\) = { }, ponieważ żaden uczeń nie uczęszcza na wszystkie trzy zajęcia. Spójrz na zacienioną część powyższego diagramu Venna.
Jak przedstawić zbiór uczniów uczęszczających na zajęcia z tańca i malarstwa?
Odpowiedź:
\(D \cap P =\) {Jan}
\(n(D \cap P) = 1\)