Você vai aprender:
Um diagrama de Venn é um diagrama que mostra a relação entre conjuntos que compartilham algo em comum. Esses diagramas descrevem elementos como pontos em um plano e conjuntos como regiões dentro da curva fechada (geralmente um círculo).
O diagrama de Venn é uma forma esquemática de representar os elementos de um conjunto ou grupo. Agora como já aprendemos set e suas propriedades. Vamos tentar apresentar conjuntos usando o diagrama de Venn.
Exemplo: Há 10 alunos em uma classe. Alguns alunos se matricularam em aulas extracurriculares como pintura, natação, música e dança.
Aqui o conjunto Universal representa os alunos da turma. O conjunto Universal é um conjunto que contém todos os objetos ou elementos e dos quais outros conjuntos são subconjuntos.
U = {John, Sam, Lee, Mary, Fred, Danny, Tom, Venn, Tim, Tracy}
O conjunto de alunos que frequentam a aula de dança é D = {John, Tim, Mary, Lee} ; O número do elemento no conjunto D é 4, \(n(D) = 4\)
O conjunto de alunos que frequentam a aula de música é M = {Fred, Tracy, Tim, Danny, Tom} ; O número do elemento no conjunto M é 5, \(n(M) = 5\)
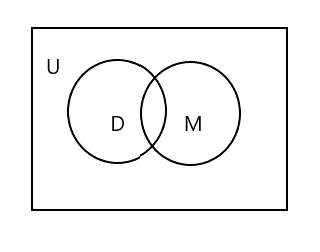
Você notará que no diagrama de Venn acima U está representando toda a área retangular. Os conjuntos D e M são representados por círculos. Os dois círculos estão se cruzando, pois têm poucos elementos em comum. Aqui 'Tim' é um elemento comum em ambos os conjuntos.
A Intersecção de conjuntos representa elementos que são comuns em ambos os conjuntos e é denotada pelo símbolo ' \(\cap\) '.
A parte sombreada no diagrama abaixo representa \(D \cap M\)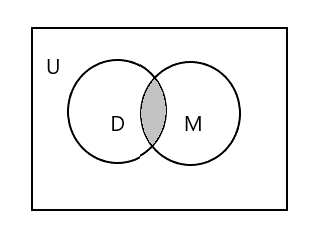
\(D \cap M = \) {Tim}
\(n(D \cap M) = 1\)
Suponha que queremos listar todos os alunos que frequentam dança ou música ou ambos.
União de dois conjuntos dados é o menor conjunto que contém todos os elementos de ambos os conjuntos. É indicado pelo símbolo 'U'. A parte sombreada no diagrama abaixo representa \(D \cup M\)
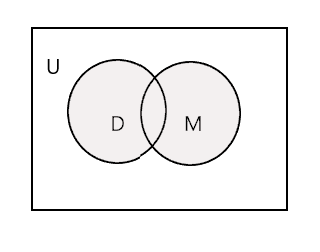
\(D \cup M =\) {John, Tim, Mary, Lee, Fred, Tracy, Danny, Tom}
\(n(D \cup M) = 8\)
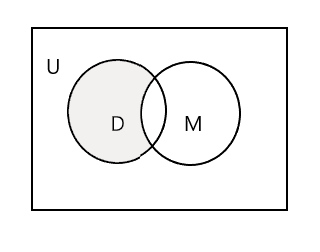
Você também pode subtrair um conjunto de outro. Aqui D - M representará o conjunto de alunos que frequentam a dança mas não a música.
\(D − M = \) { John, Mary, Lee }
\(n(D - M) = 3\)
A parte sombreada no diagrama de Venn abaixo representa D - M:
Vamos pegar o terceiro conjunto, um conjunto de alunos que frequentam a aula de pintura. P = {John, Sam, Danny, Tracy} e n(P) = 4
Diagrama de Venn para representar todos os três conjuntos:
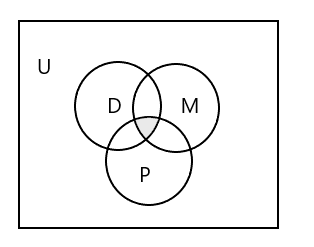
Como representar o conjunto de alunos que frequenta as três aulas?
Resposta: \(D \cap M \cap P\) = { }, pois nenhum aluno frequenta as três aulas. Observe a parte sombreada no diagrama de Venn acima.
Como representar o conjunto de alunos que frequenta as aulas de dança e pintura?
Responda:
\(D \cap P =\) {João}
\(n(D \cap P) = 1\)