Ты выучишь:
Диаграмма Венна — это диаграмма, показывающая отношения между наборами, которые имеют что-то общее. На этих диаграммах элементы изображаются в виде точек на плоскости, а множества — в виде областей внутри замкнутой кривой (обычно круга).
Диаграмма Венна — это схематический способ представления элементов набора или группы. Теперь, когда мы уже изучили множество и его свойства. Попробуем представить множества с помощью диаграммы Венна.
Пример: В классе 10 учеников. Некоторые ученики записались на внеклассные занятия, такие как рисование, плавание, музыка и танцы.
Здесь Универсальный набор представляет учащихся класса. Универсальный набор — это набор, содержащий все объекты или элементы, подмножествами которого являются другие наборы.
U = {Джон, Сэм, Ли, Мэри, Фред, Дэнни, Том, Венн, Тим, Трейси}
Набор учеников, посещающих урок танцев, равен D = {Джон, Тим, Мэри, Ли}; Количество элементов в наборе D равно 4, \(n(D) = 4\)
Набор студентов, посещающих уроки музыки, равен M = {Фред, Трейси, Тим, Дэнни, Том}; Количество элементов в множестве M равно 5, \(n(M) = 5\)
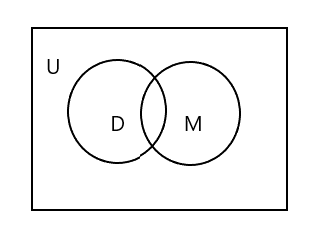
Вы заметите, что на приведенной выше диаграмме Венна U представляет всю прямоугольную область. Наборы D и M представлены кружками. Два круга пересекаются, так как у них мало общих элементов. Здесь «Тим» является общим элементом в обоих наборах.
Пересечение множеств представляет элементы, общие для обоих множеств, и обозначается символом ' \(\cap\) '.
Заштрихованная часть на диаграмме ниже представляет \(D \cap M\)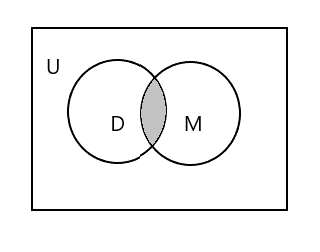
\(D \cap M = \) {Тим}
\(n(D \cap M) = 1\)
Предположим, мы хотим составить список всех студентов, которые посещают танцы, музыку или и то, и другое.
Объединение двух заданных множеств — это наименьшее множество, содержащее все элементы обоих множеств. Обозначается символом «У». Заштрихованная часть на диаграмме ниже представляет \(D \cup M\)
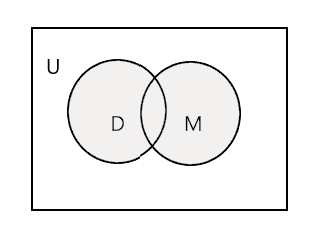
\(D \cup M =\) {Джон, Тим, Мэри, Ли, Фред, Трейси, Дэнни, Том}
\(n(D \cup M) = 8\)
Вы также можете вычесть один набор из другого. Здесь D-M будет представлять набор студентов, которые посещают танцы, но не музыку.
\(D − M = \) {Джон, Мэри, Ли}
\(n(D - M) = 3\)
Заштрихованная часть на приведенной ниже диаграмме Венна представляет D - M:
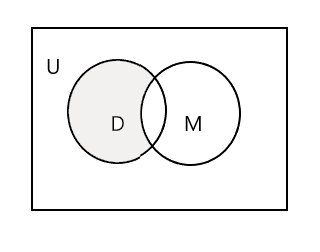
Возьмем третий набор, набор студентов, которые посещают уроки живописи. P = {Джон, Сэм, Дэнни, Трейси} и n (P) = 4
Диаграмма Венна для представления всех трех наборов:
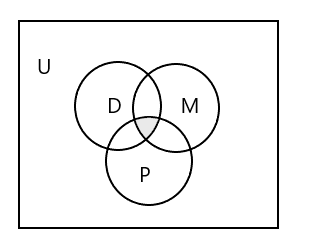
Как представить набор учащихся, посещающих все три класса?
Ответ: \(D \cap M \cap P\) = { }, так как ни один ученик не посещает все три занятия. Посмотрите на заштрихованную часть диаграммы Венна выше.
Как представить набор учеников, которые посещают уроки танцев и живописи?
Отвечать:
\(D \cap P =\) {Джон}
\(n(D \cap P) = 1\)