Ti do të mësosh:
Një diagram i Venit është një diagram që tregon marrëdhënien midis dhe midis grupeve që ndan diçka të përbashkët. Këto diagrame përshkruajnë elementet si pika në një plan dhe vendosen si rajone brenda kurbës së mbyllur (zakonisht një rreth).
Diagrami i Venit është një mënyrë skematike e paraqitjes së elementeve të një grupi ose një grupi. Tani siç kemi mësuar tashmë grupi dhe vetitë e tij. Le të përpiqemi të paraqesim grupe duke përdorur diagramin e Venit.
Shembull: Ka 10 nxënës në një klasë. Disa studentë janë regjistruar në klasa jashtëshkollore si pikturë, not, muzikë dhe kërcim.
Këtu grupi universal përfaqëson studentët e klasës. Kompleti Universal është një grup që përmban të gjitha objektet ose elementet dhe grupet e tjera të të cilit janë nënbashkësi.
U = {John, Sam, Lee, Mary, Fred, Danny, Tom, Venn, Tim, Tracy}
Grupi i studentëve që ndjekin klasën e vallëzimit është D = {John, Tim, Mary, Lee}; Numri i elementit në grupin D është 4, \(n(D) = 4\)
Grupi i studentëve që ndjekin klasën e muzikës është M = {Fred, Tracy, Tim, Danny, Tom}; Numri i elementit në grupin M është 5, \(n(M) = 5\)
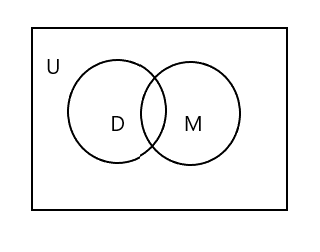
Do të vini re se në diagramin e Venit të mësipërm U përfaqëson të gjithë zonën drejtkëndore. Kompleti D dhe M përfaqësohen me rrathë. Dy rrathët kryqëzohen pasi kanë pak elementë të përbashkët. Këtu 'Tim' është një element i përbashkët në të dy grupet.
Kryqëzimi i grupeve përfaqëson elemente që janë të përbashkëta në të dy grupet dhe shënohet me simbolin ' \(\cap\) '.
Pjesa e hijezuar në diagramin më poshtë përfaqëson \(D \cap M\)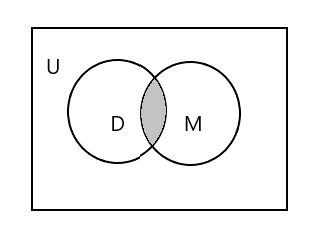
\(D \cap M = \) {Tim}
\(n(D \cap M) = 1\)
Supozoni se duam të listojmë të gjithë studentët që ndjekin vallëzim ose muzikë ose të dyja.
Bashkimi i dy grupeve të dhëna është grupi më i vogël i cili përmban të gjithë elementët e të dy grupeve. Ai shënohet me simbolin 'U'. Pjesa e hijezuar në diagramin e mëposhtëm përfaqëson \(D \cup M\)
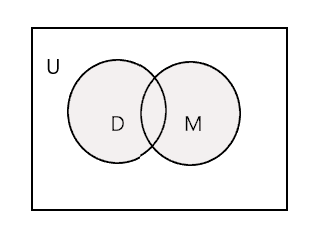
\(D \cup M =\) {John, Tim, Mary, Lee, Fred, Tracy, Danny, Tom}
\(n(D \cup M) = 8\)
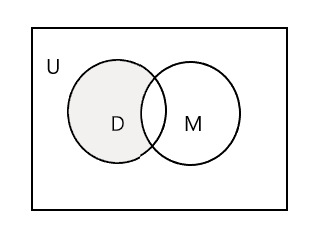
Ju gjithashtu mund të zbrisni një grup nga një tjetër. Këtu D - M do të përfaqësojë grupin e studentëve që ndjekin vallëzim, por jo muzikë.
\(D − M = \) { John, Mary, Lee }
\(n(D - M) = 3\)
Pjesa e hijezuar në diagramin e mëposhtëm të Venit përfaqëson D - M:
Le të marrim grupin e tretë, një grup studentësh që ndjekin klasën e pikturës. P = {Gjoni, Sam, Deni, Trejsi} dhe n(P) = 4
Diagrami i Venit për të përfaqësuar të tre grupet:
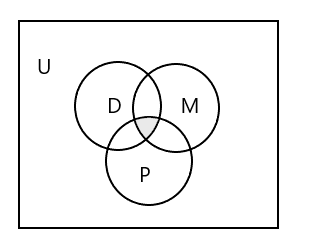
Si të përfaqësohet grupi i nxënësve që ndjekin të treja klasat?
Përgjigje: \(D \cap M \cap P\) = { }, pasi asnjë nxënës nuk ndjek të treja klasat. Shikoni pjesën e hijezuar në diagramin e mësipërm të Venit.
Si të përfaqësohet grupi i nxënësve që ndjekin klasën e kërcimit dhe pikturës?
Përgjigje:
\(D \cap P =\) {Gjoni}
\(n(D \cap P) = 1\)