Du kommer att lära dig:
Ett Venn-diagram är ett diagram som visar förhållandet mellan och mellan mängder som delar något gemensamt. Dessa diagram visar element som punkter i ett plan och uppsättningar som regioner inuti den slutna kurvan (vanligtvis en cirkel).
Venndiagram är ett schematiskt sätt att representera elementen i en mängd eller en grupp. Nu som vi redan lärt oss set och dess egenskaper. Låt oss försöka presentera uppsättningar med hjälp av Venn-diagram.
Exempel: Det är 10 elever i en klass. Vissa elever har anmält sig till extrakurser som målning, simning, musik och dans.
Här representerar Universal set elever i klassen. Den universella uppsättningen är en uppsättning som innehåller alla objekt eller element och av vilka andra uppsättningar är delmängder.
U = {John, Sam, Lee, Mary, Fred, Danny, Tom, Venn, Tim, Tracy}
Uppsättningen av elever som deltar i dansklass är D = {John, Tim, Mary, Lee} ; Antalet element i mängden D är 4, \(n(D) = 4\)
Uppsättningen av elever som deltar i musikklassen är M = {Fred, Tracy, Tim, Danny, Tom} ; Antalet element i mängden M är 5, \(n(M) = 5\)
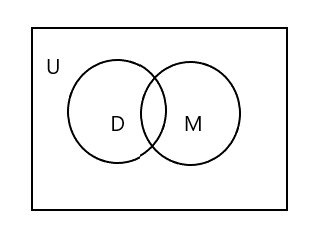
Du kommer att märka att i ovanstående Venn-diagram representerar U hela det rektangulära området. D- och M-uppsättningen representeras av cirklar. De två cirklarna skär varandra eftersom de har få element gemensamma. Här är 'Tim' ett gemensamt element i båda uppsättningarna.
Skärningen av mängder representerar element som är gemensamma i båda uppsättningarna och betecknas med symbolen ' \(\cap\) .
Den skuggade delen i diagrammet nedan representerar \(D \cap M\)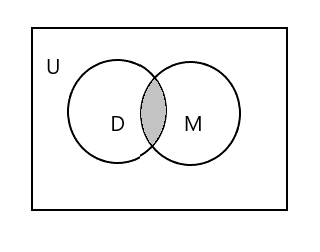
\(D \cap M = \) {Tim}
\(n(D \cap M) = 1\)
Anta att vi vill lista alla elever som går antingen till dans eller musik eller båda.
Union av två givna uppsättningar är den minsta uppsättningen som innehåller alla element i båda uppsättningarna. Det betecknas med symbolen "U". Den skuggade delen i diagrammet nedan representerar \(D \cup M\)
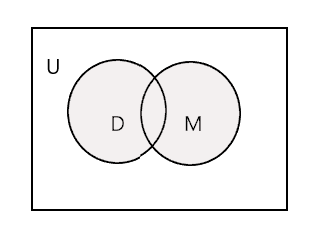
\(D \cup M =\) {John, Tim, Mary, Lee, Fred, Tracy, Danny, Tom}
\(n(D \cup M) = 8\)
Du kan också subtrahera en uppsättning från en annan. Här kommer D - M att representera uppsättningen elever som går på dans men inte musik.
\(D − M = \) { John, Mary, Lee }
\(n(D - M) = 3\)
Den skuggade delen i Venn-diagrammet nedan representerar D - M:
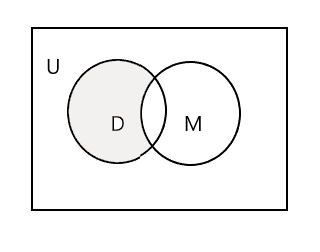
Låt oss ta den tredje uppsättningen, en uppsättning elever som går på målarkurs. P = {John, Sam, Danny, Tracy} och n(P) = 4
Venn-diagram för att representera alla tre uppsättningarna:
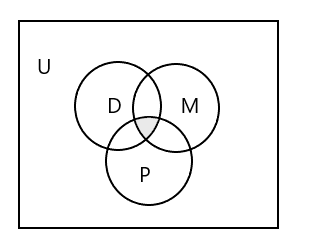
Hur representerar man uppsättningen elever som går i alla tre klasserna?
Svar: \(D \cap M \cap P\) = { }, eftersom ingen elev går i alla tre klasserna. Titta på den skuggade delen i ovanstående Venn-diagram.
Hur representerar man uppsättningen elever som går på dans- och målarkurser?
Svar:
\(D \cap P =\) {John}
\(n(D \cap P) = 1\)