คุณจะได้เรียนรู้:
ไดอะแกรมเวนน์ เป็นไดอะแกรมที่แสดงความสัมพันธ์ระหว่างและระหว่างเซตที่มีบางสิ่งร่วมกัน ไดอะแกรมเหล่านี้แสดงองค์ประกอบเป็นจุดในระนาบและกำหนดเป็นขอบเขตภายในเส้นโค้งปิด (โดยปกติจะเป็นวงกลม)
แผนภาพเวนน์เป็นแผนภาพแทนองค์ประกอบของชุดหรือกลุ่ม เมื่อเราได้เรียนรู้เซตและคุณสมบัติของมันไปแล้ว ลองนำเสนอชุดโดยใช้แผนภาพเวนน์
ตัวอย่าง: มีนักเรียน 10 คนในชั้นเรียน นักเรียนบางคนลงทะเบียนเรียนในชั้นเรียนนอกหลักสูตร เช่น การวาดภาพ ว่ายน้ำ ดนตรีและการเต้นรำ
ชุดยูนิเวอร์แซลเป็นตัวแทนของนักเรียนในชั้นเรียน เซตสากลคือเซตที่มีวัตถุหรือองค์ประกอบทั้งหมด และเซตอื่นเป็นเซตย่อย
U = {จอห์น แซม ลี แมรี่ เฟร็ด แดนนี่ ทอม เวนน์ ทิม เทรซี่}
ชุดนักเรียนที่เรียนเต้นคือ D = {John, Tim, Mary, Lee} ; จำนวนองค์ประกอบในชุด D คือ 4, \(n(D) = 4\)
ชุดนักเรียนที่เข้าชั้นเรียนดนตรีคือ M = {Fred, Tracy, Tim, Danny, Tom} ; จำนวนองค์ประกอบในชุด M คือ 5, \(n(M) = 5\)
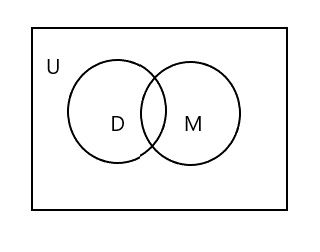
คุณจะสังเกตเห็นว่าในแผนภาพเวนน์ด้านบน U เป็นตัวแทนของพื้นที่สี่เหลี่ยมทั้งหมด ชุด D และ M แทนด้วยวงกลม วงกลมสองวงตัดกันเนื่องจากมีองค์ประกอบบางอย่างที่เหมือนกัน 'ทิม' เป็นองค์ประกอบทั่วไปในทั้งสองฉาก
อินเตอร์เซกชัน ของเซตแสดงถึงองค์ประกอบที่เหมือนกันในทั้งสองเซต และแสดงด้วยสัญลักษณ์ ' \(\cap\) '
ส่วนที่แรเงาในแผนภาพด้านล่างแสดงถึง \(D \cap M\)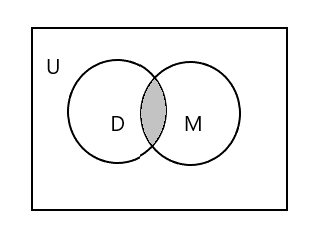
\(D \cap M = \) {ทิม}
\(n(D \cap M) = 1\)
สมมติว่าเราต้องการรายชื่อนักเรียนทุกคนที่เรียนเต้นรำหรือดนตรีหรือทั้งสองอย่าง
ยูเนี่ยน ของสองเซตที่กำหนดเป็นเซตที่เล็กที่สุดซึ่งมีสมาชิกทั้งหมดของทั้งสองเซต มันแสดงด้วยสัญลักษณ์ 'U' ส่วนที่แรเงาในแผนภาพด้านล่างแสดงถึง \(D \cup M\)
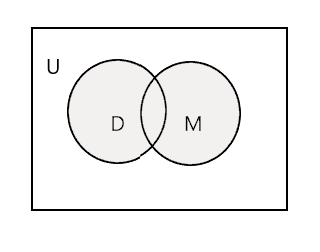
\(D \cup M =\) {จอห์น ทิม แมรี่ ลี เฟร็ด เทรซี่ แดนนี่ ทอม}
\(n(D \cup M) = 8\)
คุณยังสามารถ ลบ ชุดหนึ่งออกจากอีกชุดหนึ่งได้ ในที่นี้ D - M จะเป็นตัวแทนของกลุ่มนักเรียนที่เรียนเต้นแต่ ไม่ได้ เรียนดนตรี
\(D − M = \) { จอห์น แมรี่ ลี }
\(n(D - M) = 3\)
ส่วนที่แรเงาในแผนภาพเวนน์ด้านล่างแสดงถึง D - M :
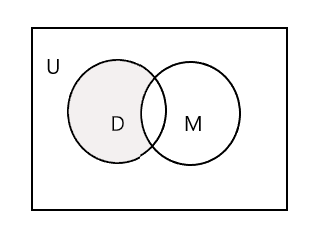
มาชุดที่ 3 ชุดนักเรียนที่เข้าคลาสวาดภาพ P = {John, Sam, Danny, Tracy} และ n(P) = 4
แผนภาพเวนน์แทนชุดทั้งสามชุด:
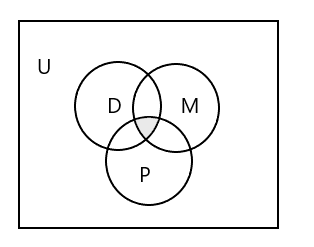
จะแสดงชุดของนักเรียนที่เข้าเรียนทั้งสามชั้นเรียนได้อย่างไร
คำตอบ: \(D \cap M \cap P\) = { } เนื่องจากไม่มีนักเรียนคนใดเข้าชั้นเรียนทั้งสามคาบ ดูส่วนที่แรเงาในแผนภาพเวนน์ด้านบน
จะเป็นตัวแทนของชุดนักเรียนที่เข้าเรียนวิชานาฏศิลป์และจิตรกรรมได้อย่างไร?
คำตอบ:
\(D \cap P =\) {จอห์น}
\(n(D \cap P) = 1\)