Matututo ka:
Ang Venn diagram ay isang diagram na nagpapakita ng ugnayan sa pagitan ng at sa pagitan ng mga set na may pagkakapareho. Ang mga diagram na ito ay naglalarawan ng mga elemento bilang mga punto sa isang eroplano at itinatakda bilang mga rehiyon sa loob ng saradong kurba (karaniwan ay isang bilog).
Ang Venn diagram ay isang eskematiko na paraan ng pagkatawan sa mga elemento ng isang set o isang grupo. Ngayon dahil natutunan na natin ang set at ang mga katangian nito. Subukan nating ipakita ang mga set gamit ang Venn diagram.
Halimbawa: Mayroong 10 mag-aaral sa isang klase. Ang ilang mga mag-aaral ay nag-enroll sa kanilang mga sarili sa mga extracurricular na klase tulad ng pagpipinta, paglangoy, musika at sayaw.
Dito kinakatawan ng Universal set ang mga mag-aaral ng klase. Ang Universal set ay isang set na naglalaman ng lahat ng bagay o elemento at kung saan ang iba pang set ay mga subset.
U = {John, Sam, Lee, Mary, Fred, Danny, Tom, Venn, Tim, Tracy}
Ang hanay ng mga estudyanteng dadalo sa dance class ay D = {John, Tim, Mary, Lee} ; Bilang ng elemento sa set D ay 4, \(n(D) = 4\)
Ang hanay ng mga mag-aaral na pumapasok sa klase ng musika ay M = {Fred, Tracy, Tim, Danny, Tom} ; Bilang ng elemento sa set M ay 5, \(n(M) = 5\)
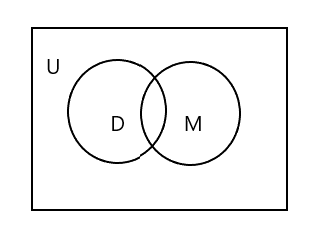
Mapapansin mo na sa itaas na Venn diagram ang U ay kumakatawan sa buong hugis-parihaba na lugar. Ang D at M set ay kinakatawan ng mga bilog. Ang dalawang bilog ay nagsasalubong dahil kakaunti ang mga elementong magkakatulad. Narito ang 'Tim' ay isang karaniwang elemento sa parehong set.
Ang Intersection ng mga hanay ay kumakatawan sa mga elemento na karaniwan sa parehong mga hanay at ipinapahiwatig ng simbolong ' \(\cap\) '.
Ang may kulay na bahagi sa diagram sa ibaba ay kumakatawan sa \(D \cap M\)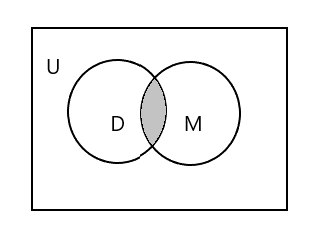
\(D \cap M = \) {Tim}
\(n(D \cap M) = 1\)
Ipagpalagay na gusto naming ilista ang lahat ng mga mag-aaral na dumalo sa alinman sa sayaw o musika o pareho.
Ang unyon ng dalawang ibinigay na hanay ay ang pinakamaliit na hanay na naglalaman ng lahat ng elemento ng parehong hanay. Ito ay tinutukoy ng simbolong 'U'. Ang may kulay na bahagi sa diagram sa ibaba ay kumakatawan sa \(D \cup M\)
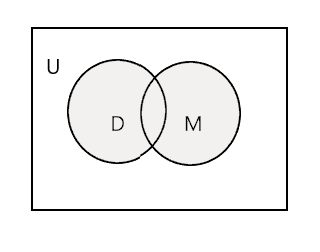
\(D \cup M =\) {John, Tim, Mary, Lee, Fred, Tracy, Danny, Tom}
\(n(D \cup M) = 8\)
Maaari mo ring ibawas ang isang set mula sa isa pa. Dito kakatawanin ng D - M ang hanay ng mga mag-aaral na dumalo sa sayaw ngunit hindi sa musika.
\(D − M = \) { John, Mary, Lee }
\(n(D - M) = 3\)
Ang may kulay na bahagi sa ibaba ng Venn diagram ay kumakatawan sa D - M :
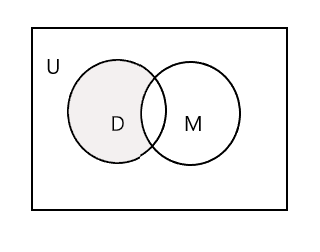
Kunin natin ang ikatlong set, isang set ng mga mag-aaral na dumalo sa klase ng pagpipinta. P = {John, Sam, Danny, Tracy} at n(P) = 4
Venn diagram upang kumatawan sa lahat ng tatlong set:
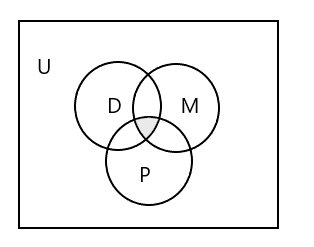
Paano kinakatawan ang hanay ng mga mag-aaral na pumapasok sa lahat ng tatlong klase?
Sagot: \(D \cap M \cap P\) = { }, dahil walang estudyanteng pumapasok sa lahat ng tatlong klase. Tingnan ang may kulay na bahagi sa Venn diagram sa itaas.
Paano kinakatawan ang hanay ng mga mag-aaral na dumadalo sa klase ng sayaw at pagpipinta?
Sagot:
\(D \cap P =\) {John}
\(n(D \cap P) = 1\)