Öğreneceksiniz:
Venn diyagramı , ortak bir noktayı paylaşan kümeler arasındaki ve arasındaki ilişkiyi gösteren bir diyagramdır. Bu diyagramlar, öğeleri bir düzlemdeki noktalar olarak gösterir ve kümeleri kapalı eğri (genellikle bir daire) içindeki bölgeler olarak gösterir.
Venn diyagramı, bir kümenin veya grubun elemanlarını şematik olarak temsil etmenin bir yoludur. Şimdi kümeyi ve özelliklerini öğrendiğimiz gibi. Kümeleri Venn diyagramını kullanarak sunmaya çalışalım.
Örnek: Bir sınıfta 10 öğrenci vardır. Bazı öğrenciler kendilerini resim, yüzme, müzik ve dans gibi ders dışı derslere kaydettirdiler.
Burada Evrensel küme, sınıfın öğrencilerini temsil etmektedir. Evrensel küme, tüm nesneleri veya öğeleri içeren ve diğer kümelerin alt kümeler olduğu bir kümedir.
U = {John, Sam, Lee, Mary, Fred, Danny, Tom, Venn, Tim, Tracy}
Dans dersine katılan öğrencilerin kümesi D = {John, Tim, Mary, Lee} ; D kümesindeki eleman sayısı 4, \(n(D) = 4\)
Müzik dersine katılan öğrencilerin kümesi M = {Fred, Tracy, Tim, Danny, Tom} ; M kümesindeki eleman sayısı 5, \(n(M) = 5\)
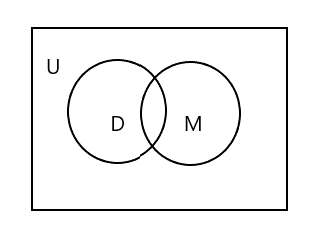
Yukarıdaki Venn şemasında U'nun tüm dikdörtgen alanı temsil ettiğini fark edeceksiniz. D ve M kümesi dairelerle temsil edilir. İki daire, çok az ortak öğeye sahip oldukları için kesişiyor. Burada 'Tim' her iki sette de ortak bir unsurdur.
Kümelerin Kesişimi , her iki kümede de ortak olan öğeleri temsil eder ve ' \(\cap\) ' sembolü ile gösterilir.
Aşağıdaki diyagramdaki gölgeli kısım \(D \cap M\) temsil eder.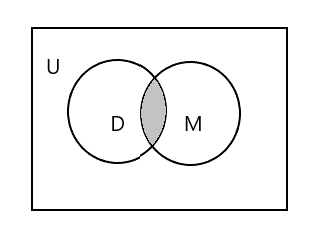
\(D \cap M = \) {Tim}
\(n(D \cap M) = 1\)
Diyelim ki dansa, müziğe veya her ikisine birden katılan tüm öğrencileri listelemek istiyoruz.
Verilen iki kümenin birleşimi, her iki kümenin tüm öğelerini içeren en küçük kümedir. 'U' sembolü ile gösterilir. Aşağıdaki diyagramdaki gölgeli kısım \(D \cup M\) temsil eder.
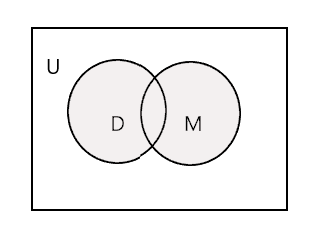
\(D \cup M =\) {John, Tim, Mary, Lee, Fred, Tracy, Danny, Tom}
\(n(D \cup M) = 8\)
Ayrıca bir seti diğerinden çıkarabilirsiniz . Burada D - M , dansa katılan ancak müziğe katılmayan öğrenci grubunu temsil edecek.
\(D − M = \) { John, Mary, Lee }
\(n(D - M) = 3\)
Aşağıdaki Venn şemasındaki gölgeli kısım, D - M'yi temsil eder:
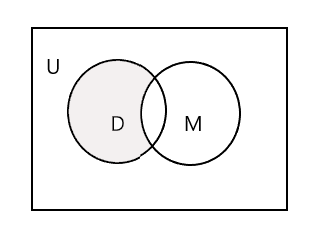
Resim kursuna giden bir grup öğrenci olan üçüncü grubu ele alalım. P = {John, Sam, Danny, Tracy} ve n(P) = 4
Üç kümeyi de temsil eden Venn diyagramı:
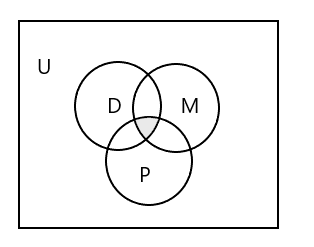
Üç derse de devam eden öğrenciler kümesi nasıl temsil edilir?
Yanıt: \(D \cap M \cap P\) = { }, hiçbir öğrenci üç sınıfın tamamına katılmadığı için. Yukarıdaki Venn şemasındaki gölgeli kısma bakın.
Dans ve resim dersine devam eden öğrenciler kümesi nasıl temsil edilir?
Cevap:
\(D \cap P =\) {John}
\(n(D \cap P) = 1\)