Ти навчишся:
Діаграма Венна — це діаграма, яка показує зв’язок між наборами, які мають щось спільне. Ці діаграми зображують елементи як точки на площині та множини як області всередині замкнутої кривої (зазвичай кола).
Діаграма Венна — це схематичний спосіб представлення елементів множини або групи. Тепер, як ми вже вивчили множину та її властивості. Спробуємо представити множини за допомогою діаграми Венна.
Приклад: у класі 10 учнів. Деякі учні записалися на позакласні заняття, такі як малювання, плавання, музика та танці.
Тут універсальний набір представляє учнів класу. Універсальна множина — це множина, що містить усі об’єкти або елементи, а інші множини є підмножинами.
U = {Джон, Сем, Лі, Мері, Фред, Денні, Том, Венн, Тім, Трейсі}
Набір студентів, які відвідують танцювальний клас, D = {Джон, Тім, Мері, Лі} ; Кількість елементів у наборі D дорівнює 4, \(n(D) = 4\)
Набір студентів, які відвідують уроки музики: M = {Фред, Трейсі, Тім, Денні, Том} ; Кількість елементів у наборі M дорівнює 5, \(n(M) = 5\)
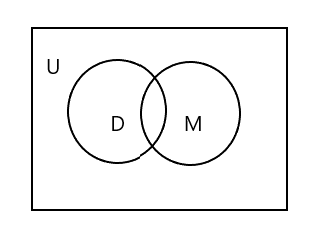
Ви помітите, що на наведеній вище діаграмі Венна U представляє всю прямокутну область. Набір D і M представлено кружками. Два кола перетинаються, оскільки вони мають мало спільних елементів. Тут «Тім» є загальним елементом в обох наборах.
Перетин множин представляє елементи, які є спільними в обох множинах, і позначається символом ' \(\cap\) '.
Заштрихована частина на діаграмі нижче позначає \(D \cap M\)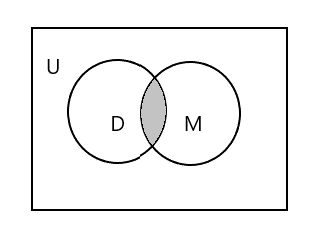
\(D \cap M = \) {Тім}
\(n(D \cap M) = 1\)
Припустімо, ми хочемо перерахувати всіх студентів, які відвідують або танці, або музику, або обидва.
Об'єднання двох даних множин - це найменша множина, яка містить усі елементи обох множин. Позначається символом «U». Заштрихована частина на діаграмі нижче позначає \(D \cup M\)
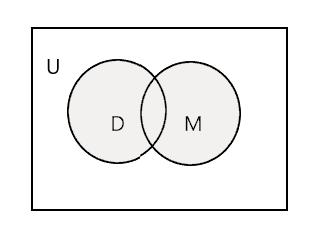
\(D \cup M =\) {Джон, Тім, Мері, Лі, Фред, Трейсі, Денні, Том}
\(n(D \cup M) = 8\)
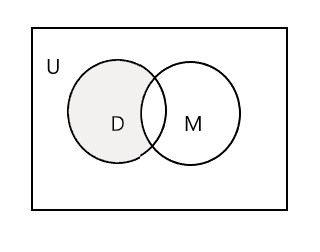
Ви також можете відняти один набір від іншого. Тут D - M представлятиме групу студентів, які відвідують танці, але не займаються музикою.
\(D − M = \) { Джон, Мері, Лі }
\(n(D - M) = 3\)
Заштрихована частина на діаграмі Венна нижче позначає D - M:
Давайте візьмемо третю групу, групу студентів, які відвідують уроки живопису. P = {Джон, Сем, Денні, Трейсі} і n(P) = 4
Діаграма Венна для представлення всіх трьох наборів:
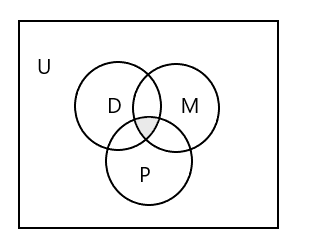
Як представити набір студентів, які відвідують усі три класи?
Відповідь: \(D \cap M \cap P\) = { }, оскільки жоден учень не відвідує всі три класи. Подивіться на заштриховану частину на діаграмі Венна вище.
Як представити набір студентів, які відвідують уроки танців і малювання?
відповідь:
\(D \cap P =\) {Іван}
\(n(D \cap P) = 1\)