Siz o'rganasiz:
Venn diagrammasi - bu umumiy bir narsaga ega bo'lgan to'plamlar orasidagi va o'rtasidagi munosabatni ko'rsatadigan diagramma. Ushbu diagrammalar elementlarni tekislikdagi nuqtalar sifatida tasvirlaydi va yopiq egri chiziq ichidagi mintaqalar (odatda aylana) sifatida o'rnatiladi.
Venn diagrammasi to'plam yoki guruh elementlarini sxematik tasvirlash usulidir. Endi biz allaqachon to'plam va uning xususiyatlarini bilib oldik. Keling, Venn diagrammasi yordamida to'plamlarni taqdim etishga harakat qilaylik.
Misol: Bir sinfda 10 nafar o‘quvchi bor. Ba'zi talabalar rasm, suzish, musiqa va raqs kabi sinfdan tashqari darslarga yozildi.
Bu erda Universal to'plam sinf o'quvchilarini ifodalaydi. Universal to'plam barcha ob'ektlar yoki elementlarni o'z ichiga olgan va boshqa to'plamlar kichik to'plamlar bo'lgan to'plamdir.
U = {Jon, Sem, Li, Meri, Fred, Denni, Tom, Venn, Tim, Treysi}
Raqs darsiga qatnashayotgan talabalar to‘plami D = {Jon, Tim, Meri, Li} ; D to‘plamdagi elementlar soni 4, \(n(D) = 4\)
Musiqa darsiga qatnaydigan talabalar toʻplami M = {Fred, Tracy, Tim, Denny, Tom} ; M to‘plamdagi elementlar soni 5, \(n(M) = 5\)
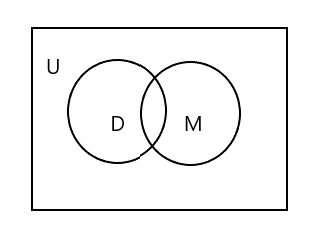
Yuqoridagi Venn diagrammasida U butun to'rtburchaklar maydonni ifodalaganini ko'rasiz. D va M to'plam doiralar bilan ifodalanadi. Ikki doira kesishadi, chunki ular bir nechta umumiy elementlarga ega. Bu erda "Tim" ikkala to'plamdagi umumiy elementdir.
To'plamlar kesishmasi ikkala to'plamda umumiy bo'lgan elementlarni ifodalaydi va ' \(\cap\) ' belgisi bilan belgilanadi.
Quyidagi diagrammadagi soyali qism \(D \cap M\) ifodalaydi.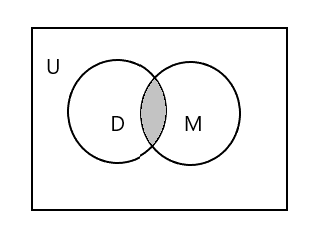
\(D \cap M = \) {Tim}
\(n(D \cap M) = 1\)
Aytaylik, biz raqsga, musiqaga yoki ikkalasiga ham qatnashadigan barcha talabalarni sanab o'tmoqchimiz.
Berilgan ikkita toʻplamning birlashuvi ikkala toʻplamning barcha elementlarini oʻz ichiga olgan eng kichik toʻplamdir. U "U" belgisi bilan belgilanadi. Quyidagi diagrammadagi soyali qism \(D \cup M\) ifodalaydi.
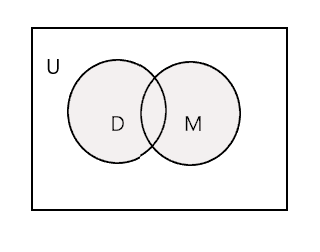
\(D \cup M =\) {Jon, Tim, Meri, Li, Fred, Treysi, Denni, Tom}
\(n(D \cup M) = 8\)
Bundan tashqari, bir to'plamdan boshqasini ayirishingiz mumkin. Bu erda D - M musiqa emas , balki raqsga qatnashadigan talabalar to'plamini ifodalaydi.
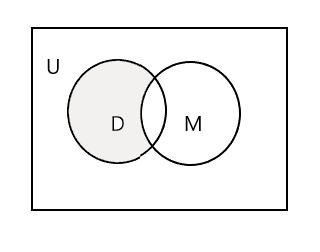
\(D − M = \) { Jon, Meri, Li }
\(n(D - M) = 3\)
Quyidagi Venn diagrammasidagi soyali qism D - M ni ifodalaydi:
Keling, uchinchi to'plamni, rasm darsiga qatnashadigan talabalar to'plamini olaylik. P = {Jon, Sem, Denni, Treysi} va n (P) = 4
Venn diagrammasi barcha uchta to'plamni ifodalaydi:
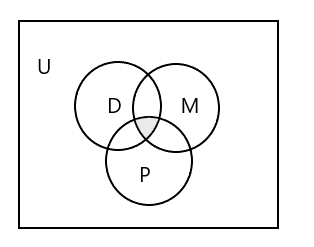
Uchta sinfda qatnashadigan talabalar to'plamini qanday ifodalash mumkin?
Javob: \(D \cap M \cap P\) = { }, chunki uchala sinfga ham o‘quvchi qatnashmaydi. Yuqoridagi Venn diagrammasidagi soyali qismga qarang.
Raqs va rasm darsiga qatnashayotgan o'quvchilar to'plamini qanday ifodalash mumkin?
Javob:
\(D \cap P =\) {Jon}
\(n(D \cap P) = 1\)