Back to the topics list

تعبير جبري

محتويات:

• ما هو المتغير؟
• أنواع التعبيرات الجبرية.
• معامل في الرياضيات او درجة.
• مثل وخلافا للشروط.
• متعدد الحدود.
• الجمع والطرح والضرب والقسمة في التعبير الجبري.
• تطبيق قاعدة ترتيب العمليات لتبسيط التعبير الجبري.

أرقام حرفية

في الجبر نستخدم الحروف الهجائية الإنجليزية أو اليونانية مثل أ ، ب ، س ، ص ، β ، Φ ، ... لتمثيل الأرقام. تستخدم هذه الأحرف لتمثيل كميات غير معروفة. نظرًا لأن الأحرف تمثل الأرقام ، فإنها تسمى أرقامًا حرفية. يمكن أن يحمل الرقم الحرفي أي قيمة ومن ثم نسميه متغيرًا . يسمى الرقم ذو القيمة المحددة بالثابت.

تعبير جبري

يُطلق على مجموعة الثوابت والقيم الحرفية (المتغيرات) المتصلة بعملية حسابية واحدة أو أكثر (الجمع ، الضرب ، الطرح ، القسمة) تعبيرًا جبريًا. علامة واحدة أو أكثر (+ ، -) تقسم التعبير الجبري إلى عدة أجزاء. يسمى كل جزء مع علامته مصطلح من التعبير الجبري. يمكن أن يكون المصطلح ثابتًا مثل 4 على سبيل المثال ، متغير ، على سبيل المثال ، x ، منتج ثابت ومتغير ، على سبيل المثال ، 4x أو منتج من متغيرين أو أكثر ، على سبيل المثال ، xy ، xy ² .

أحادي: التعبير الجبري الذي له مصطلح واحد فقط يسمى أحادي الحد. مثال: 7x، ab ² ، 8
ذو الحدين: يُطلق على التعبير الجبري الذي له حدان اسم ذو الحدين. مثال: x ² + y ² ، x + 2
ثلاثي الحدود: يُطلق على التعبير الجبري الذي يحتوي على ثلاثة مصطلحات اسم ثلاثي الحدود. مثال: x ² + y ² + z ² ، x + y +2

معامل في الرياضيات او درجة

كل من الكميات (ثابتة أو حرفية) مضروبة لتشكيل منتج يسمى عامل المنتج وأي عامل في المنتج يسمى معامل حاصل ضرب العوامل المتبقية. في المصطلح ، -11p ² q من التعبير 5p ^{3-11p 2 q} + 7 ،

• المعامل العددي هو -11.
• المعامل الحرفي هو p ² q.
• معامل p ² هو -11q.
• المعامل -11p ² هو q.
  

مثل وخلافا للشروط

يُقال إن مصطلحات التعبير الجبري التي لها نفس المتغير (المتغيرات) ونفس الأس (الأسس) للمتغيرات تكون متشابهة. يمكن أن يختلف المصطلح المتشابه فقط في المعاملات.
2xy + 3x + 4y + 5xy + 7y
المصطلحان 2xy و 5xy متشابهان. 4y و 7y متشابهان.

لا تتشابه الحدود في التعبير الجبري 2x + 3xy + 5y.

متعدد الحدود

يُطلق على التعبير الجبري الذي تكون فيه قوى المتغيرات المعنية أعدادًا صحيحة غير سالبة متعدد الحدود.

\(x^3+ x^2 + 2x + 1\) متعدد الحدود في متغير واحد x.
\(6x - \frac{4x}{y} + 2y + 3 \) ليس متعدد الحدود (لاحظ أن y في المصطلح الثاني لديه قوة -1)

جمع وطرح المصطلحات المتشابهة

لدمج الحدود المتشابهة عن طريق الجمع أو الطرح ، ما عليك سوى إضافة أو طرح المعاملات العددية للمصطلحات المحددة.
مثال:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

جمع وطرح التعبيرات الجبرية

لإضافة تعبير جبري ، ما عليك سوى إضافة مصطلحاتهم المتشابهة. للراحة ، اكتب المصطلح المشابه واحدًا أسفل الآخر في نفس العمود. مثال:
يضيف -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) ، \(2x + 4xy + y\) ، \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

للطرح ، اقلب علامة كل حد من التعبير الذي يتم طرحه ثم اجمع التعبيرين معًا. مثال
اطرح \(3x^2 + 5x + 7y^2\) من \(9x^2 + 7x + 5y + 10y^2\)

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

يمكنك أيضًا إضافة أو طرح التعبيرات الجبرية باستخدام التجميع. لنأخذ المثال أعلاه ونطرح باستخدام التجميع:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

ضرب التعابير الجبرية

يمكن تقسيم عملية ضرب التعبير الجبري إلى ثلاث حالات ، فلنناقشها بشكل منفصل:

قضية أنا (Multiplication of Monomials) : اضرب معاملاتهم العددية معًا ثم المتغيرات بإضافة أسس المتغيرات الشائعة ، مع ترك المتغيرات غير الشائعة دون تغيير. مثال: أوجد حاصل ضرب 6bc و 5b = \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

قضية ثانيًا (ضرب كثير الحدود في حد أحادي): اضرب كل حد من كثير الحدود في monomial . مثال: حاصل ضرب 3xy و x ² + 2xy + y ² هو
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

قضية ثالثا (ضرب كثير الحدود بواسطة متعدد الحدود) : اضرب كل حد من كثير الحدود بكل حد من الآخر ثم اجمع المصطلحات المتشابهة لتبسيط حاصل الضرب. مثال: حاصل ضرب (2x + 3y) و (x + y + 2) هو
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

تقسيم التعبيرات الجبرية

يمكن تفسير تقسيم التعبير الجبري باستخدام الحالات الثلاث أدناه.

قضية أنا (قسمة المونومال على المونومال) : لتقسيم المونومال على المونومال ، أوجد حاصل معاملاتهم العددية وحاصل قسمة المتغيرات بطرح الأسس للمتغيرات الشائعة.
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

قضية ثانيًا (قسمة كثير الحدود على حدي) : قسّم كل حد من كثير الحدود على أحادي ثم قسّمه كما هو مذكور في الحالة أعلاه.
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

قضية ثالثا ( قسمة كثير الحدود على كثير الحدود ): سيتم ذلك بطريقة القسمة المطولة. دعونا نحاول فهم هذا باستخدام مثال.
\(8x^2 + 9x - 8 \div 8x + 1\)

ابدأ بقسمة الحد الأول من المقسوم (8x ² ) على الحد الأول من المقسوم عليه (8x) لإيجاد الحد الأول من حاصل القسمة (x) ، ثم اضرب حد خارج القسمة مع المقسوم عليه وطرحه.

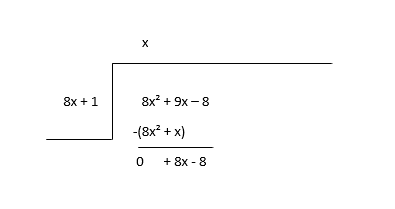
اعتبر الباقي بمثابة توزيعات أرباح جديدة وقم بتقدير المدة التالية للحاصل.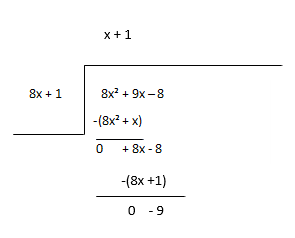

الحاصل - س + 1 ، الباقي - -9

إزالة الأقواس واستخدام قاعدة ترتيب العمليات

لتبسيط تعبير جبري يحتوي على أقواس ، قم بإزالة الأقواس بالترتيب:

مثال:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)