Back to the topics list

cəbri ifadə

İçindəkilər:

• Dəyişən nədir?
• Cəbri ifadənin növləri.
• Əmsal.
• Bəyənmə və Bəyənmə Şərtləri.
• Polinom.
• Cəbri ifadənin toplama, çıxma, vurma və bölmə.
• Cəbri ifadəni sadələşdirmək üçün Əməliyyatların Sırası qaydasının tətbiqi.

Hərfi Rəqəmlər

Cəbrdə rəqəmləri təmsil etmək üçün a, b, x, y, β, Φ, ... kimi ingilis və ya yunan əlifbalarından istifadə edirik. Bu hərflər naməlum kəmiyyətləri göstərmək üçün istifadə olunur. Hərflər rəqəmləri ifadə etdiyi üçün hərfi rəqəmlər adlanır. Hərfi nömrə istənilən dəyəri qəbul edə bilər, ona görə də biz onu dəyişən adlandırırıq. Müəyyən bir dəyəri olan ədəd sabit adlanır.

Cəbri ifadə

Bir və ya bir neçə arifmetik əməliyyatla (toplama, vurma, çıxma, bölmə) birləşdirilən sabitlərin və literalların (dəyişənlərin) birləşməsinə cəbri ifadə deyilir. Bir və ya bir neçə işarə (+, −) cəbri ifadəni bir neçə hissəyə bölür. İşarəsi olan hər bir hissə cəbri ifadənin termini adlanır. Termin məsələn, 4, dəyişən, məsələn, x, sabit və dəyişənin hasili, məsələn, 4x və ya iki və ya daha çox dəyişənin hasili, məsələn, xy, xy ² ola bilər.

Monomial: Yalnız bir üzvü olan cəbri ifadəyə monomial deyilir. Misal: 7x, ab ² , 8
Binom: İki şərti olan cəbri ifadəyə binom deyilir. Misal: x ² + y ² , x + 2
Üçbucaqlı: Üç üzvü olan cəbri ifadəyə üçhədli deyilir. Misal: x ² + y ² + z ² , x +y +2

Əmsal

Məhsul yaratmaq üçün vurulan kəmiyyətlərin hər biri (sabit və ya hərf) məhsulun amili, məhsuldakı hər hansı bir amil isə qalan amillərin məhsulunun əmsalı adlanır. Termində 5p ³ − 11p ² q + 7 ifadəsinin -11p ² q,

• Rəqəmsal əmsalı -11-dir.
• Hərfi əmsalı p ² q-dir.
• p ² əmsalı -11q-dir.
• -11p ² əmsalı q-dir.
  

Bəyənmə və Bəyənmə Şərtləri

Dəyişənlərin eyni dəyişən(ləri) və eyni göstərici(lər)i olan cəbri ifadənin şərtlərinə terminlər kimi deyilir. Bənzər termin yalnız əmsallarda fərqlənə bilər.
2xy+ 3x + 4y + 5xy + 7y
2xy və 5xy terminləri terminlər kimidir. 4y və 7y terminləri kimidir.

2x + 3xy + 5y cəbri ifadəsindəki terminlərin hamısı fərqlidir.

Polinom

İştirak edən dəyişənlərin səlahiyyətlərinin mənfi olmayan tam ədədlər olduğu cəbri ifadə çoxhədli adlanır.

\(x^3+ x^2 + 2x + 1\) bir x dəyişənində çoxhədlidir.
\(6x - \frac{4x}{y} + 2y + 3 \) çoxhədli deyil (diqqət yetirin ki, ikinci hədddəki y -1 gücünə malikdir)

Bənzər şərtlərin toplanması və çıxılması

Bənzər şərtləri toplama və ya çıxma yolu ilə birləşdirmək üçün sadəcə verilmiş şərtlərin ədədi əmsallarını əlavə edin və ya çıxarın.
Misal:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

Cəbri ifadələrin toplanması və çıxılması

Cəbri ifadə əlavə etmək üçün sadəcə onların oxşar şərtlərini əlavə edin. Rahatlıq üçün eyni sütunda oxşar termini bir-birinin altına yazın. Misal:
Əlavə et -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) , \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

Çıxarma üçün, çıxarılan ifadənin hər bir termininin işarəsini çevirin və sonra iki ifadəni birləşdirin. Misal
\(9x^2 + 7x + 5y + 10y^2\) \)-dən \ \(3x^2 + 5x + 7y^2\) .

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

Siz həmçinin Qruplaşdırmadan istifadə edərək cəbri ifadələri əlavə edə və ya çıxara bilərsiniz. Yuxarıdakı nümunəni götürək və Qruplaşdırmadan istifadə edərək çıxaq:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

Cəbri ifadələrin vurulması

Cəbri ifadənin vurulmasını üç halda bölmək olar, gəlin onları ayrıca müzakirə edək:

Case I (Monomialların vurulması) : Onların ədədi əmsallarını, sonra isə ümumi dəyişənlərin eksponentlərini əlavə etməklə dəyişənləri çarpın, qeyri-adi dəyişənləri dəyişməz buraxın. Misal: 6bc və 5b = məhsulunu tapın \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

Case II (Çoxhədlinin Monomiala vurulması) : Çoxhədlinin hər bir həddini monomiala vurun. Misal: 3xy və x ² + 2xy + y ² -nin hasili
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

Case III (Çoxhədlinin çoxhədli ilə vurulması) : Bir çoxhədlinin hər bir üzvünü digərinin hər həddi ilə çoxaldın və sonra hasili sadələşdirmək üçün oxşar şərtləri birləşdirin. Nümunə: (2x + 3y) və (x + y + 2) hasilidir
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

Cəbri ifadələrin bölməsi

Cəbri ifadənin bölünməsi aşağıda üç halda izah edilə bilər.

Case I (Monomialın Monomiala bölünməsi) : Monomialı monomiala bölmək üçün ümumi dəyişənlərin göstəricilərini çıxmaqla onların ədədi əmsallarının hissələrini və dəyişənlərin əmsallarını tapın. Misal:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

Case II (Çoxhədlinin Monomiala bölünməsi) : Çoxhədlinin hər həddini monohədəyə bölün və sonra yuxarıdakı halda verildiyi kimi bölün. Misal:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

Case III ( Çoxhədlinin Çoxhədli ilə Bölünməsi ): Bu uzun bölmə üsulu ilə ediləcək. Bir misaldan istifadə edərək bunu anlamağa çalışaq.
\(8x^2 + 9x - 8 \div 8x + 1\)

Dividendin birinci həddini (8x ² ) bölmənin (8x) birinci həddi ilə bölməklə başlayın və bölmənin (x) birinci həddini tapın və sonra bölmənin müddətini bölənlə vurub çıxın.

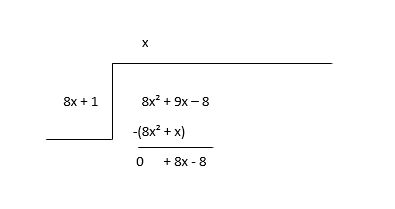
Qalanı yeni dividend hesab edin və bölmənin növbəti müddətini təxmin edin.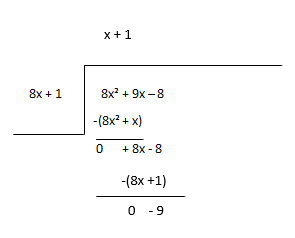

Hissə - x + 1, Qalan - -9

Mötərizənin çıxarılması və Əməliyyatlar Qaydasının istifadəsi

Mötərizədə olan cəbri ifadəni sadələşdirmək üçün mötərizələri aşağıdakı ardıcıllıqla çıxarın:

Misal:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)