Back to the topics list

বীজগাণিতিক এক্সপ্রেশন

বিষয়বস্তু:

• একটি পরিবর্তনশীল কি?
• বীজগাণিতিক রাশির ধরন।
• গুণাঙ্ক.
• লাইক এবং আনলাইক শর্তাবলী।
• বহুপদ।
• বীজগণিতীয় রাশির যোগ, বিয়োগ, গুণ ও ভাগ।
• বীজগাণিতিক রাশি সরলীকরণের জন্য অপারেশনের নিয়মের প্রয়োগ।

আক্ষরিক সংখ্যা

বীজগণিতে আমরা সংখ্যার প্রতিনিধিত্ব করতে ইংরেজি বা গ্রীক বর্ণমালা যেমন a, b, x, y, β, Φ, ... ব্যবহার করি। এই অক্ষরগুলি অজানা পরিমাণের প্রতিনিধিত্ব করতে ব্যবহৃত হয়। যেহেতু অক্ষর সংখ্যার প্রতিনিধিত্ব করে তাই তাদের আক্ষরিক সংখ্যা বলা হয়। একটি আক্ষরিক সংখ্যা যে কোনও মান ধরে নিতে পারে তাই আমরা এটিকে একটি পরিবর্তনশীল বলি। একটি নির্দিষ্ট মান সহ একটি সংখ্যাকে ধ্রুবক বলে।

বীজগাণিতিক এক্সপ্রেশন

এক বা একাধিক গাণিতিক ক্রিয়াকলাপ (যোগ, গুণ, বিয়োগ, ভাগ) দ্বারা সংযুক্ত ধ্রুবক এবং আক্ষরিক (ভেরিয়েবল) এর সংমিশ্রণকে বীজগণিতীয় রাশি বলা হয়। এক বা একাধিক চিহ্ন (+, −) একটি বীজগণিতিক রাশিকে কয়েকটি অংশে বিভক্ত করে। চিহ্ন সহ প্রতিটি অংশকে বীজগাণিতিক রাশির একটি শব্দ বলা হয়। একটি শব্দ একটি ধ্রুবক হতে পারে যেমন 4, একটি চলক, উদাহরণস্বরূপ, x, একটি ধ্রুবক এবং পরিবর্তনশীলের একটি গুণফল, উদাহরণস্বরূপ, 4x বা দুই বা ততোধিক চলকের একটি গুণফল, উদাহরণস্বরূপ, xy, xy ² ।

মনোমিয়াল: যে বীজগণিতীয় রাশিতে একটিমাত্র পদ থাকে তাকে একপদ বলে। উদাহরণ: 7x, ab ² , 8
দ্বিপদ: যে বীজগণিতীয় রাশিতে দুটি পদ থাকে তাকে দ্বিপদ বলে। উদাহরণ: x ² + y ² , x + 2
ত্রিনমিক: যে বীজগণিতীয় রাশিতে তিনটি পদ থাকে তাকে ত্রিনমীয় বলে। উদাহরণ: x ² + y ² + z ² , x +y +2

গুণাঙ্ক

প্রতিটি রাশি (ধ্রুবক বা আক্ষরিক) গুণিত করে একটি গুণফল তৈরি করে, তাকে পণ্যের একটি গুণনীয়ক বলা হয় এবং একটি পণ্যের যে কোনো গুণনীয়ককে অবশিষ্ট গুণনীয়কের গুণফলের সহগ বলা হয়। পরিভাষায়, 5p ³ − 11p ² q + 7 অভিব্যক্তিটির -11p ² q,

• সংখ্যাগত সহগ হল -11।
• আক্ষরিক সহগ হল p ² q।
• p ² এর সহগ হল -11q।
• -11p ² এর সহগ হল q।
  

লাইক এবং আনলাইক শর্তাবলী

ভেরিয়েবলের একই চলক(গুলি) এবং একই সূচক(গুলি) বিশিষ্ট বীজগণিতীয় রাশির পদগুলিকে পদের মতো বলা হয়। লাইক টার্ম শুধুমাত্র সহগ পার্থক্য হতে পারে.
2xy+ 3x + 4y + 5xy + 7y
2xy এবং 5xy পদগুলি পদের মতো। 4y এবং 7y শব্দের মতো।

বীজগাণিতিক রাশি 2x + 3xy + 5y এর পদগুলি সবই অসদৃশ।

বহুপদ

একটি বীজগণিতীয় রাশি যাতে জড়িত চলকের শক্তিগুলি অ-ঋণাত্মক পূর্ণসংখ্যা হয় তাকে বহুপদ বলা হয়।

\(x^3+ x^2 + 2x + 1\) x একটি চলকের একটি বহুপদ।
\(6x - \frac{4x}{y} + 2y + 3 \) একটি বহুপদ নয় (লক্ষ্য করুন যে দ্বিতীয় পদে y-এর শক্তি -1)

লাইক পদের যোগ ও বিয়োগ

যোগ বা বিয়োগ দ্বারা মত পদগুলিকে একত্রিত করতে, প্রদত্ত পদগুলির সংখ্যাগত সহগ যোগ বা বিয়োগ করুন।
উদাহরণ:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

বীজগাণিতিক রাশির যোগ ও বিয়োগ

বীজগাণিতিক রাশি যোগ করতে, কেবল পদের মতো তাদের যোগ করুন। সুবিধার জন্য একই কলামে একটির নিচের মত শব্দটি লিখুন। উদাহরণ:
যোগ করুন -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) , \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

বিয়োগের জন্য, বিয়োগ করা অভিব্যক্তিটির প্রতিটি পদের চিহ্নটি ফ্লিপ করুন এবং তারপরে দুটি রাশি একসাথে যোগ করুন। উদাহরণ
\(9x^2 + 7x + 5y + 10y^2\) \(3x^2 + 5x + 7y^2\) বিয়োগ করুন

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

আপনি গ্রুপিং ব্যবহার করে বীজগাণিতিক রাশি যোগ বা বিয়োগ করতে পারেন। আসুন উপরের উদাহরণটি গ্রহণ করি এবং গ্রুপিং ব্যবহার করে বিয়োগ করি:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

বীজগাণিতিক রাশির গুন

বীজগাণিতিক রাশির গুণকে তিনটি ক্ষেত্রে ভাগ করা যায়, আসুন আলাদাভাবে আলোচনা করা যাক:

মামলা আমি (মনোমিয়ালের গুণ) : তাদের সংখ্যাসূচক সহগকে একসাথে গুণ করুন এবং তারপরে সাধারণ চলকের সূচক যোগ করে, অস্বাভাবিক চলকগুলি অপরিবর্তিত রেখে চলকগুলিকে গুণ করুন। উদাহরণ: 6bc এবং 5b = এর গুণফল নির্ণয় কর \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

মামলা ২ (একপদ দ্বারা বহুপদী গুণ) : বহুপদীর প্রতিটি পদকে একপদ দ্বারা গুণ করুন। উদাহরণ: 3xy এবং x ² + 2xy + y ² এর গুণফল
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

মামলা III (বহুপদ দ্বারা বহুপদীর গুণ) : একটি বহুপদীর প্রতিটি পদকে অন্যটির প্রতিটি পদ দ্বারা গুণ করুন এবং তারপর গুণফলকে সরল করার জন্য অনুরূপ পদগুলিকে একত্রিত করুন। উদাহরণ: (2x + 3y) এবং (x + y + 2) এর গুণফল
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

বীজগাণিতিক রাশির বিভাজন

বীজগাণিতিক রাশির বিভাজন নীচে তিনটি ক্ষেত্রে ব্যবহার করে ব্যাখ্যা করা যেতে পারে।

মামলা আমি (একটি মনোমিয়াল দ্বারা একটি মনোমিয়ালের বিভাজন) : একটি মনোমিয়ালকে একটি মনোমিয়াল দ্বারা ভাগ করতে, সাধারণ চলকের সূচকগুলি বিয়োগ করে তাদের সংখ্যাসূচক সহগ এবং ভেরিয়েবলের ভাগফল নির্ণয় করুন৷ উদাহরণ:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

মামলা ২ (একপদ দ্বারা বহুপদীর বিভাজন) : বহুপদীর প্রতিটি পদকে একপদ দিয়ে ভাগ করুন এবং তারপরে উপরের ক্ষেত্রে দেওয়া হিসাবে ভাগ করুন। উদাহরণ:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

মামলা III ( একটি বহুপদ দ্বারা বহুপদ বিভাজন ): এটি দীর্ঘ বিভাজন পদ্ধতি দ্বারা সম্পন্ন করা হবে। আসুন একটি উদাহরণ ব্যবহার করে এটি বোঝার চেষ্টা করি।
\(8x^2 + 9x - 8 \div 8x + 1\)

ভাগফল(x) এর প্রথম পদ খুঁজে পেতে ভাজকের (8x) প্রথম পদের সাথে লভ্যাংশের প্রথম পদ (8x ² ) ভাগ করে শুরু করুন এবং তারপর আপনি ভাগফল পদটিকে ভাজকের সাথে গুণ করুন এবং বিয়োগ করুন।

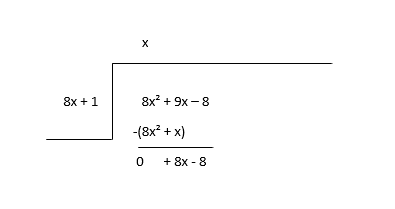
অবশিষ্টকে নতুন লভ্যাংশ হিসাবে বিবেচনা করুন এবং ভাগফলের পরবর্তী মেয়াদ অনুমান করুন।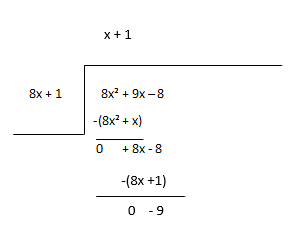

ভাগফল - x + 1, অবশিষ্ট - -9

বন্ধনী অপসারণ এবং অপারেশন বিধি আদেশ ব্যবহার

বন্ধনী সমন্বিত একটি বীজগণিতীয় রাশিকে সরল করতে, বন্ধনীগুলিকে এই ক্রমে সরিয়ে দিন:

উদাহরণ:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)