In der Algebra verwenden wir englische oder griechische Alphabete wie a, b, x, y, β, Φ, ..., um Zahlen darzustellen. Diese Buchstaben werden verwendet, um unbekannte Größen darzustellen. Da Buchstaben Zahlen darstellen, werden sie als Literalzahlen bezeichnet. Eine Literalzahl kann jeden Wert annehmen, daher nennen wir sie eine Variable . Eine Zahl mit einem bestimmten Wert heißt Konstante.
Eine Kombination aus Konstanten und Literalen (Variablen), die durch eine oder mehrere arithmetische Operationen (Addition, Multiplikation, Subtraktion, Division) verbunden sind, wird als algebraischer Ausdruck bezeichnet. Ein oder mehrere Zeichen (+, −) zerlegen einen algebraischen Ausdruck in mehrere Teile. Jeder Teil mit seinem Vorzeichen wird als Term des algebraischen Ausdrucks bezeichnet. Ein Term kann eine Konstante wie beispielsweise 4, eine Variable wie beispielsweise x, ein Produkt aus einer Konstanten und einer Variablen wie beispielsweise 4x oder ein Produkt aus zwei oder mehr Variablen wie beispielsweise xy, xy 2 sein.
Monom: Ein algebraischer Ausdruck, der nur einen Term hat, wird Monom genannt. Beispiel: 7x, ab 2 , 8
Binomial: Ein algebraischer Ausdruck, der zwei Terme hat, wird Binomial genannt. Beispiel: x 2 + y 2 , x + 2
Trinom: Ein algebraischer Ausdruck mit drei Termen wird als Trinom bezeichnet. Beispiel: x 2 + y 2 + z 2 , x + y +2
Jede der Größen (Konstante oder Literale), die multipliziert wird, um ein Produkt zu bilden, wird als Faktor des Produkts bezeichnet, und jeder Faktor in einem Produkt wird als Koeffizient des Produkts der verbleibenden Faktoren bezeichnet. Im Ausdruck -11p 2 q des Ausdrucks 5p 3 − 11p 2 q + 7,
Die Terme des algebraischen Ausdrucks mit derselben(n) Variable(n) und demselben(n) Exponent(en) der Variablen werden als gleiche Terme bezeichnet. Gleiche Terme können sich nur in Koeffizienten unterscheiden.
2xy + 3x + 4y + 5xy + 7y
Die Terme 2xy und 5xy sind wie Terme. 4y und 7y sind wie Begriffe.
Terme im algebraischen Ausdruck 2x + 3xy + 5y sind alle ungleich.
Ein algebraischer Ausdruck, bei dem die Potenzen der beteiligten Variablen nicht negative ganze Zahlen sind, wird als Polynom bezeichnet.
\(x^3+ x^2 + 2x + 1\) ist ein Polynom in einer Variablen x.
\(6x - \frac{4x}{y} + 2y + 3 \) ist kein Polynom (beachten Sie, dass y im zweiten Term die Potenz -1 hat)
Um gleiche Terme durch Addition oder Subtraktion zu kombinieren, addieren oder subtrahieren Sie einfach die numerischen Koeffizienten der gegebenen Terme.
Beispiel:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)
Um algebraische Ausdrücke hinzuzufügen, fügen Sie einfach ihre ähnlichen Terme hinzu. Schreiben Sie der Einfachheit halber gleiche Begriffe untereinander in dieselbe Spalte. Beispiel:
Hinzufügen -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) \(x^2\; + 2x + 3xy + 6y + 3y^2\)
Subtrahiere \(3x^2 + 5x + 7y^2\) von \(9x^2 + 7x + 5y + 10y^2\)
Die Multiplikation des algebraischen Ausdrucks kann in drei Fälle unterteilt werden, lassen Sie uns sie separat besprechen:
Fall
Fall
Fall
Die Aufteilung des algebraischen Ausdrucks kann anhand der folgenden drei Fälle erklärt werden.
Fall
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(8x^2 + 9x - 8 \div 8x + 1\)
Beginnen Sie damit, den ersten Term des Dividenden (8x 2 ) durch den ersten Term des Divisors (8x) zu dividieren, um den ersten Term des Quotienten (x) zu finden, und dann multiplizieren Sie den Quotiententerm mit dem Divisor und subtrahieren.
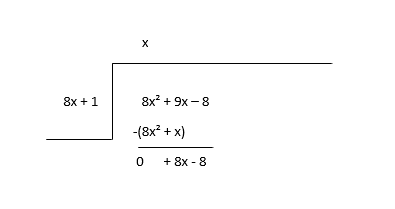
Betrachten Sie den Rest als neuen Dividenden und schätzen Sie den nächsten Term des Quotienten. 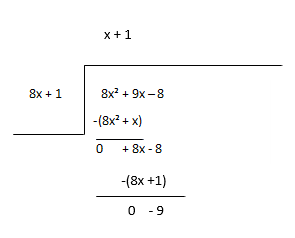
Quotient - x + 1, Rest - -9
Um einen algebraischen Ausdruck mit Klammern zu vereinfachen, entfernen Sie die Klammern in der folgenden Reihenfolge:
Beispiel: