In Algebra we use English or Greek Alphabets like a, b, x, y, β, Φ, ... to represent numbers. These letters are used to represent unknown quantities. Since letters represent numbers so they are called literal numbers. A literal number can assume any value hence we call it a variable. A number with a definite value is called a constant.
A combination of constants and literals(variables) connected by one or more arithmetic operations(addition, multiplication, subtraction, division) is called an Algebraic expression. One or more signs (+, −) break an algebraic expression into several parts. Each part with its sign is called a term of the algebraic expression. A term can be a constant like for example 4, a variable, for example, x, a product of a constant and variable, for example, 4x or a product of two or more variables, for example, xy, xy2.
Monomial: An algebraic expression that has only one term is called a monomial. Example: 7x, ab2, 8
Binomial: An algebraic expression that has two terms is called a binomial. Example: x2 + y2, x + 2
Trinomial: An algebraic expression that has three terms is called a trinomial. Example: x2 + y2 + z2, x +y +2
Each of the quantities(constant or literals) multiplied to form a product, is called a factor of the product and any factor in a product is called the coefficient of the product of the remaining factors. In the term, -11p2q of the expression 5p3 − 11p2q + 7,
The terms of the algebraic expression having the same variable(s) and same exponent(s) of the variables are said to be like terms. Like term can differ only in coefficients.
2xy+ 3x + 4y + 5xy + 7y
The terms 2xy and 5xy are like terms. 4y and 7y are like terms.
Terms in the algebraic expression 2x + 3xy + 5y are all unlike.
An algebraic expression in which the powers of the variables involved are non-negative integers is called a polynomial.
\(x^3+ x^2 + 2x + 1\) is a polynomial in one variable x.
\(6x - \frac{4x}{y} + 2y + 3 \) is not a polynomial (notice that y in the second term has power -1)
To combine like terms by addition or subtraction, simply add or subtract the numerical coefficients of the given terms.
Example:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)
To add algebraic expression, simply add theirs like terms. For convenience write the like term one below the other in the same column. Example:
Add -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) , \(x^2\; + 2x + 3xy + 6y + 3y^2\)
Subtract \(3x^2 + 5x + 7y^2\) from \(9x^2 + 7x + 5y + 10y^2\)
Multiplication of algebraic expression can be divided into three cases, let's discuss them separately:
Case
Case
Case
Division of algebraic expression can be explained using below three cases.
Case
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(8x^2 + 9x - 8 \div 8x + 1\)
Begin by dividing the first term of the dividend(8x2) with the first term of the divisor(8x) to find the first term of the quotient(x) and then you multiply the quotient term with the divisor and subtract.
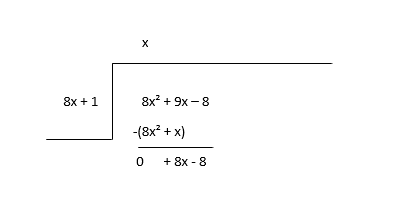
Consider the remainder as the new dividend and estimate the next term of the quotient.
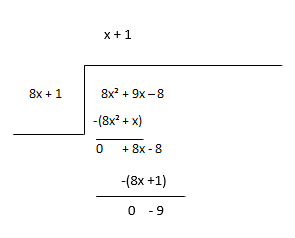
Quotient - x + 1, Remainder - -9
To simplify an algebraic expression containing brackets, remove the brackets in the order of :
Example: