Back to the topics list

expresión algebraica

Contenido:

• ¿Qué es una variable?
• Tipos de expresiones algebraicas.
• Coeficiente.
• Términos similares y diferentes.
• Polinomio.
• Suma, Resta, Multiplicación y División de Expresión Algebraica.
• Aplicación de la regla del Orden de las Operaciones para simplificar expresiones algebraicas.

números literales

En álgebra usamos alfabetos ingleses o griegos como a, b, x, y, β, Φ, ... para representar números. Estas letras se utilizan para representar cantidades desconocidas. Como las letras representan números, se llaman números literales. Un número literal puede asumir cualquier valor, por lo que lo llamamos variable . Un número con un valor definido se llama constante.

Expresión algebraica

Una combinación de constantes y literales (variables) conectadas por una o más operaciones aritméticas (suma, multiplicación, resta, división) se llama expresión algebraica. Uno o más signos (+, −) dividen una expresión algebraica en varias partes. Cada parte con su signo se llama término de la expresión algebraica. Un término puede ser una constante como por ejemplo 4, una variable, por ejemplo, x, un producto de una constante y una variable, por ejemplo, 4x o un producto de dos o más variables, por ejemplo, xy, xy ² .

Monomio: Una expresión algebraica que tiene un solo término se llama monomio. Ejemplo: 7x, ab ² , 8
Binomial: Una expresión algebraica que tiene dos términos se llama binomial. Ejemplo: x ² + y ² , x + 2
Trinomio: Una expresión algebraica que tiene tres términos se llama trinomio. Ejemplo: x ² + y ² + z ² , x + y +2

Coeficiente

Cada una de las cantidades (constantes o literales) multiplicadas para formar un producto, se llama factor del producto y cualquier factor en un producto se llama coeficiente del producto de los factores restantes. En el término, -11p ² q de la expresión 5p ³ − 11p ² q + 7,

• El coeficiente numérico es -11.
• El coeficiente literal es p ² q.
• El coeficiente de p ² es -11q.
• El coeficiente de -11p ² es q.
  

Términos similares y diferentes

Los términos de la expresión algebraica que tienen la(s) misma(s) variable(s) y el(los) mismo(s) exponente(s) de las variables se dice que son términos semejantes. Los términos iguales pueden diferir solo en los coeficientes.
2xy+ 3x + 4y + 5xy + 7y
Los términos 2xy y 5xy son términos semejantes. 4y y 7y son términos semejantes.

Los términos en la expresión algebraica 2x + 3xy + 5y son todos diferentes.

Polinomio

Una expresión algebraica en la que las potencias de las variables involucradas son números enteros no negativos se llama polinomio.

\(x^3+ x^2 + 2x + 1\) es un polinomio en una variable x.
\(6x - \frac{4x}{y} + 2y + 3 \) no es un polinomio (nota que y en el segundo término tiene potencia -1)

Suma y resta de términos semejantes

Para combinar términos semejantes por suma o resta, simplemente suma o resta los coeficientes numéricos de los términos dados.
Ejemplo:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

Suma y Resta de Expresiones Algebraicas

Para agregar una expresión algebraica, simplemente agregue los términos semejantes. Por conveniencia escriba el término semejante uno debajo del otro en la misma columna. Ejemplo:
Agregar -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) , \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

Para la resta , invierta el signo de cada término de la expresión que se resta y luego sume las dos expresiones. Ejemplo
Resta \(3x^2 + 5x + 7y^2\) de \(9x^2 + 7x + 5y + 10y^2\)

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

También puede sumar o restar expresiones algebraicas usando Agrupación. Tomemos el ejemplo anterior y restemos usando Agrupación:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

Multiplicación de Expresiones Algebraicas

La multiplicación de expresiones algebraicas se puede dividir en tres casos, analicémoslos por separado:

Caso yo (Multiplicación de Monomios) : Multiplica sus coeficientes numéricos juntos y luego las variables sumando los exponentes de las variables comunes, dejando las variables no comunes sin cambios. Ejemplo: Encuentra el producto de 6bc y 5b = \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

Caso II (Multiplicación de polinomio por un monomio) : Multiplica cada término del polinomio por el monomio. Ejemplo: Producto de 3xy y x ² + 2xy + y ² es
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

Caso tercero (Multiplicación de un polinomio por polinomio) : Multiplica cada término de un polinomio por cada término del otro y luego combina los términos similares para simplificar el producto. Ejemplo: Producto de (2x + 3y) y (x + y + 2) es
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

División de Expresiones Algebraicas

La división de la expresión algebraica se puede explicar usando los siguientes tres casos.

Caso yo (División de un Monomio por un Monomio) : Para dividir un monomio por un monomio, encuentre los cocientes de sus coeficientes numéricos y los cocientes de las variables restando los exponentes de las variables comunes.Ejemplo:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

Caso II (División de polinomio por monomio) : divida cada término del polinomio por un monomio y luego divida como se indica en el caso anterior. Ejemplo:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

Caso tercero ( División de un Polinomio por un Polinomio ): Esto se hará por el método de división larga. Tratemos de entender esto usando un ejemplo.
\(8x^2 + 9x - 8 \div 8x + 1\)

Comience dividiendo el primer término del dividendo (8x ² ) con el primer término del divisor (8x) para encontrar el primer término del cociente (x) y luego multiplique el término del cociente con el divisor y reste.

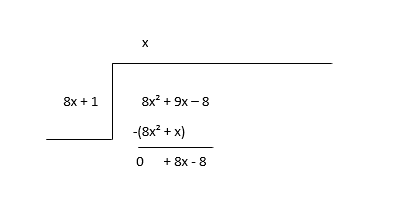
Considere el resto como el nuevo dividendo y estime el próximo término del cociente.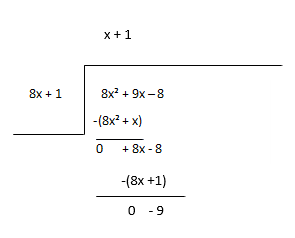

Cociente - x + 1, Resto - -9

Eliminación de corchetes y uso de la regla del orden de las operaciones

Para simplificar una expresión algebraica que contiene corchetes, elimine los corchetes en el orden de:

Ejemplo:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)