Back to the topics list

عبارت جبری

فهرست:

• متغیر چیست؟
• انواع بیان جبری
• ضریب.
• شرایط لایک و عدم دوست داشتن.
• چند جمله ای.
• جمع، تفریق، ضرب و تقسیم عبارت جبری.
• استفاده از قانون ترتیب عملیات برای ساده سازی بیان جبری.

اعداد تحت اللفظی

در جبر از الفبای انگلیسی یا یونانی مانند a، b، x، y، β، φ، ... برای نمایش اعداد استفاده می کنیم. این حروف برای نمایش مقادیر ناشناخته استفاده می شوند. از آنجایی که حروف نشان دهنده اعداد هستند، به آنها اعداد تحت اللفظی می گویند. یک عدد تحت اللفظی می تواند هر مقداری را در نظر بگیرد، از این رو آن را متغیر می نامیم. عددی با مقدار معین را ثابت می نامند.

عبارت جبری

ترکیبی از ثابت ها و لفظ ها (متغیرها) که توسط یک یا چند عملیات حسابی (جمع، ضرب، تفریق، تقسیم) به هم متصل شده اند، عبارت جبری نامیده می شود. یک یا چند علامت (+، −) یک عبارت جبری را به چند قسمت تقسیم می کند. هر جزء با علامت خود اصطلاحی از عبارت جبری نامیده می شود. یک عبارت می تواند ثابت باشد مانند مثال 4، یک متغیر، به عنوان مثال، x، حاصلضرب یک ثابت و متغیر، برای مثال، 4x یا حاصلضرب دو یا چند متغیر، به عنوان مثال، xy، xy ² .

یک جمله: به عبارت جبری که فقط یک جمله دارد، یک جمله می گویند. مثال: 7x، ab ² ، 8
دو جمله ای: به عبارت جبری که دارای دو جمله باشد، دو جمله ای می گویند. مثال: x ² + y ² , x + 2
سه جمله ای: به عبارت جبری که دارای سه جمله باشد، سه جمله ای می گویند. مثال: x ² + y ² + z ² , x +y +2

ضریب

هر یک از مقادیر (ثابت یا لفظی) ضرب شده برای تشکیل یک محصول، ضریب حاصل و هر عاملی در یک محصول را ضریب حاصلضرب عوامل باقیمانده می نامند. در اصطلاح، -11p ² q از عبارت 5p ³ − 11p ² q + 7،

• ضریب عددی 11- است.
• ضریب تحت اللفظی p ² q است.
• ضریب p ² -11q است.
• ضریب -11p ² q است.
  

شرایط لایک و عدم دوست داشتن

اصطلاحات عبارت جبری که دارای متغیر(های) یکسان و توان(های) یکسان متغیرها هستند، مانند اصطلاحات گفته می شود. عبارت Like فقط در ضرایب می تواند متفاوت باشد.
2xy + 3x + 4y + 5xy + 7y
اصطلاحات 2xy و 5xy مانند اصطلاحات هستند. 4y و 7y مانند اصطلاح هستند.

اصطلاحات در عبارت جبری 2x + 3xy + 5y همگی متفاوت هستند.

چند جمله ای

یک عبارت جبری که در آن توان متغیرهای درگیر اعداد صحیح غیر منفی باشد، چند جمله ای نامیده می شود.

\(x^3+ x^2 + 2x + 1\) یک چند جمله ای در یک متغیر x است.
\(6x - \frac{4x}{y} + 2y + 3 \) یک چند جمله ای نیست (توجه کنید که y در جمله دوم دارای توان -1 است)

جمع و تفریق اصطلاحات مانند

برای ترکیب عبارت‌های مشابه با جمع یا تفریق، کافی است ضرایب عددی عبارت‌های داده شده را جمع یا تفریق کنید.
مثال:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

جمع و تفریق عبارات جبری

برای افزودن عبارت جبری، به سادگی عبارت آنها را مانند عبارت اضافه کنید. برای راحتی، عبارت مشابه را یکی زیر دیگری در همان ستون بنویسید. مثال:
اضافه کردن -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) \(2x + 4xy + y\) \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

برای تفریق ، علامت هر جمله عبارتی که در حال تفریق است را برگردانید و سپس دو عبارت را با هم جمع کنید. مثال
کم کردن \(3x^2 + 5x + 7y^2\) از \(9x^2 + 7x + 5y + 10y^2\)

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

همچنین می توانید عبارات جبری را با استفاده از Grouping اضافه یا کم کنید. بیایید مثال بالا را در نظر بگیریم و با استفاده از Grouping کم کنیم:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

ضرب عبارات جبری

ضرب عبارت جبری را می توان به سه مورد تقسیم کرد، اجازه دهید آنها را جداگانه مورد بحث قرار دهیم:

مورد من (ضرب تک نامی ها) : ضرایب عددی آنها را با هم ضرب کنید و سپس متغیرها را با افزودن توان متغیرهای رایج ضرب کنید و متغیرهای غیر معمول را بدون تغییر رها کنید. مثال: حاصل ضرب 6bc و 5b = را بیابید \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

مورد II (چند جمله ای ضرب در یک جمله) : هر جمله چند جمله ای را در تک جمله ضرب کنید. مثال: حاصل ضرب 3xy و x ² + 2xy + y ² است
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

مورد III (ضرب یک چند جمله ای در چند جمله ای) : هر جمله یک چند جمله ای را در هر جمله دیگری ضرب کنید و سپس عبارت های مشابه را با هم ترکیب کنید تا حاصل ضرب را ساده کنید. مثال: حاصل ضرب (2x + 3y) و (x + y + 2) است
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

تقسیم بندی عبارات جبری

تقسیم بندی عبارت جبری را می توان با استفاده از سه حالت زیر توضیح داد.

مورد من (تقسیم یک تک اسمی بر یک تک جمله ای) : برای تقسیم یک تک جمله ای بر یک جمله، ضرایب عددی آنها و ضرایب متغیرها را با تفریق توان متغیرهای رایج پیدا کنید. مثال:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

مورد II (تقسیم چند جمله ای بر تک جمله ای) : هر جمله چند جمله ای را بر یک تک جمله ای تقسیم کنید و سپس مانند حالت فوق تقسیم کنید. مثال:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

مورد III ( تقسیم چند جمله ای به چند جمله ای ): این کار با روش تقسیم طولانی انجام می شود. بیایید سعی کنیم این را با استفاده از یک مثال درک کنیم.
\(8x^2 + 9x - 8 \div 8x + 1\)

با تقسیم اولین جمله تقسیم (8x ² ) با اولین جمله مقسوم علیه (8x) شروع کنید تا اولین جمله ضریب (x) را پیدا کنید و سپس جمله ضریب را با تقسیم کننده ضرب کنید و از آن کم کنید.

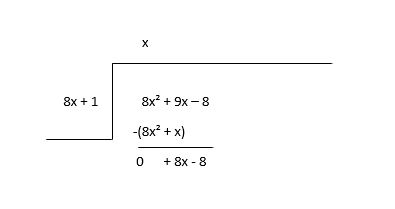
باقی مانده را به عنوان سود سهام جدید در نظر بگیرید و ترم بعدی ضریب را تخمین بزنید.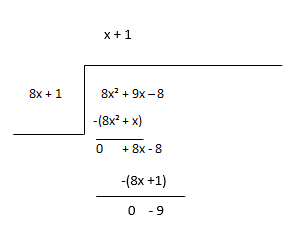

ضریب - x + 1، باقیمانده - 9

حذف براکت ها و استفاده از قانون ترتیب عملیات

برای ساده کردن یک عبارت جبری حاوی براکت، براکت ها را به ترتیب زیر حذف کنید:

مثال:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)