Back to the topics list

expression algébrique

Contenu:

• Qu'est-ce qu'une variable ?
• Types d'expression algébrique.
• Coefficient.
• Termes similaires et différents.
• Polynôme.
• Addition, soustraction, multiplication et division d'expression algébrique.
• Application de la règle d'ordre des opérations pour simplifier l'expression algébrique.

Nombres littéraux

En algèbre, nous utilisons des alphabets anglais ou grecs comme a, b, x, y, β, Φ, ... pour représenter les nombres. Ces lettres sont utilisées pour représenter des quantités inconnues. Comme les lettres représentent des nombres, on les appelle des nombres littéraux. Un nombre littéral peut prendre n'importe quelle valeur, c'est pourquoi nous l'appelons une variable . Un nombre avec une valeur définie est appelé une constante.

Expression algébrique

Une combinaison de constantes et de littéraux (variables) reliés par une ou plusieurs opérations arithmétiques (addition, multiplication, soustraction, division) est appelée une expression algébrique. Un ou plusieurs signes (+, −) divisent une expression algébrique en plusieurs parties. Chaque partie avec son signe est appelée un terme de l'expression algébrique. Un terme peut être une constante comme par exemple 4, une variable, par exemple, x, un produit d'une constante et d'une variable, par exemple, 4x ou un produit de deux variables ou plus, par exemple, xy, xy ² .

Monôme : Une expression algébrique qui n'a qu'un seul terme est appelée un monôme. Exemple : 7x, ab ² , 8
Binôme : Une expression algébrique qui a deux termes s'appelle un binôme. Exemple : x ² + y ² , x + 2
Trinôme : Une expression algébrique qui a trois termes est appelée un trinôme. Exemple : x ² + y ² + z ² , x +y +2

Coefficient

Chacune des quantités (constantes ou littérales) multipliée pour former un produit est appelée facteur du produit et tout facteur dans un produit est appelé coefficient du produit des facteurs restants. Dans le terme, -11p ² q de l'expression 5p ³ − 11p ² q + 7,

• Le coefficient numérique est -11.
• Le coefficient littéral est p ² q.
• Le coefficient de p ² est -11q.
• Le coefficient de -11p ² est q.
  

Termes similaires et différents

Les termes de l'expression algébrique ayant la ou les mêmes variables et le ou les mêmes exposants des variables sont dits semblables. Un même terme ne peut différer que par des coefficients.
2xy+ 3x + 4y + 5xy + 7y
Les termes 2xy et 5xy sont comme des termes. 4y et 7y sont comme des termes.

Les termes de l'expression algébrique 2x + 3xy + 5y sont tous différents.

Polynôme

Une expression algébrique dans laquelle les puissances des variables impliquées sont des entiers non négatifs est appelée un polynôme.

\(x^3+ x^2 + 2x + 1\) est un polynôme à une variable x.
\(6x - \frac{4x}{y} + 2y + 3 \) n'est pas un polynôme (notez que y dans le second terme a une puissance -1)

Addition et soustraction de termes similaires

Pour combiner des termes similaires par addition ou soustraction, il suffit d'ajouter ou de soustraire les coefficients numériques des termes donnés.
Exemple:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

Addition et soustraction d'expressions algébriques

Pour ajouter une expression algébrique, ajoutez simplement les leurs comme termes. Pour plus de commodité, écrivez le même terme l'un en dessous de l'autre dans la même colonne. Exemple:
Ajouter -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) , \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

Pour la soustraction , inversez le signe de chaque terme de l'expression qui est soustraite, puis additionnez les deux expressions ensemble. Exemple
Soustraire \(3x^2 + 5x + 7y^2\) de \(9x^2 + 7x + 5y + 10y^2\)

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

Vous pouvez également ajouter ou soustraire des expressions algébriques à l'aide du groupement. Prenons l'exemple ci-dessus et soustrayons en utilisant Grouping :

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

Multiplication d'expressions algébriques

La multiplication d'une expression algébrique peut être divisée en trois cas, discutons-en séparément :

Cas je (Multiplication de monômes) : Multipliez leurs coefficients numériques ensemble, puis les variables en ajoutant les exposants des variables communes, en laissant les variables peu communes inchangées. Exemple : Trouver le produit de 6bc et 5b = \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

Cas II (Multiplication d'un polynôme par un monôme) : Multipliez chaque terme du polynôme par le monôme. Exemple : Produit de 3xy et x ² + 2xy + y ² est
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

Cas III (Multiplication d'un polynôme par un polynôme) : multipliez chaque terme d'un polynôme par chaque terme de l'autre, puis combinez les termes similaires pour simplifier le produit. Exemple : Le produit de (2x + 3y) et ( x + y + 2) est
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

Division des expressions algébriques

La division de l'expression algébrique peut être expliquée en utilisant ci-dessous trois cas.

Cas je (Division d'un monôme par un monôme) : Pour diviser un monôme par un monôme, trouver les quotients de leurs coefficients numériques et les quotients des variables en soustrayant les exposants des variables communes.Exemple :
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

Cas II (Division d'un polynôme par un monôme) : Divisez chaque terme du polynôme par un monôme, puis divisez comme indiqué dans le cas ci-dessus. Exemple :
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

Cas III ( Division d'un polynôme par un polynôme ): Cela se fera par la méthode de la division longue. Essayons de comprendre cela à l'aide d'un exemple.
\(8x^2 + 9x - 8 \div 8x + 1\)

Commencez par diviser le premier terme du dividende (8x ² ) par le premier terme du diviseur (8x) pour trouver le premier terme du quotient (x) puis multipliez le terme du quotient par le diviseur et soustrayez.

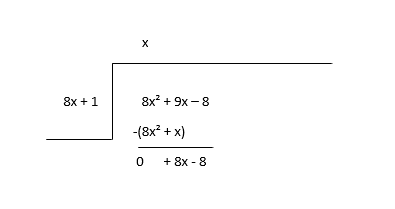
Considérez le reste comme le nouveau dividende et estimez le prochain terme du quotient.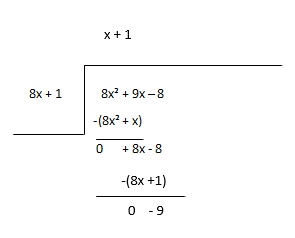

Quotient - x + 1, Reste - -9

Suppression des parenthèses et utilisation de la règle d'ordre des opérations

Pour simplifier une expression algébrique contenant des parenthèses, supprimez les parenthèses dans l'ordre suivant :

Exemple:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)