Back to the topics list

बीजगणतीय अभिव्यक्ति

सामग्री:

• एक चर क्या है?
• बीजगणितीय व्यंजकों के प्रकार।
• गुणांक।
• पसंद और विपरीत शर्तें।
• बहुपद।
• बीजगणितीय व्यंजकों का जोड़, घटाव, गुणा और भाग।
• बीजगणितीय व्यंजक को सरल बनाने के लिए संक्रियाओं के क्रम नियम का अनुप्रयोग।

शाब्दिक संख्याएँ

बीजगणित में हम संख्याओं का प्रतिनिधित्व करने के लिए अंग्रेजी या ग्रीक अक्षर जैसे a, b, x, y, β, Φ, ... का उपयोग करते हैं। इन अक्षरों का उपयोग अज्ञात राशियों को दर्शाने के लिए किया जाता है। चूँकि अक्षर संख्याओं का प्रतिनिधित्व करते हैं इसलिए उन्हें शाब्दिक संख्याएँ कहा जाता है। एक शाब्दिक संख्या कोई भी मान ग्रहण कर सकती है इसलिए हम इसे एक चर कहते हैं। एक निश्चित मान वाली संख्या को अचर कहते हैं।

बीजगणतीय अभिव्यक्ति

एक या एक से अधिक अंकगणितीय संक्रियाओं (जोड़, गुणा, घटाव, भाग) से जुड़े स्थिरांक और शाब्दिक (चर) के संयोजन को बीजगणितीय व्यंजक कहा जाता है। एक या अधिक चिह्न (+, −) बीजगणितीय व्यंजक को कई भागों में तोड़ते हैं। प्रत्येक भाग अपने चिह्न के साथ बीजगणितीय व्यंजक का पद कहलाता है। एक पद एक स्थिरांक हो सकता है जैसे उदाहरण 4 के लिए, एक चर, उदाहरण के लिए, x, एक स्थिर और चर का गुणनफल, उदाहरण के लिए, 4x या दो या दो से अधिक चरों का गुणनफल, उदाहरण के लिए, xy, xy ² ।

एकपदी: एक बीजगणितीय व्यंजक जिसमें केवल एक पद हो, एकपदी कहलाता है। उदाहरण: 7x, एबी ² , 8
द्विपद: एक बीजगणितीय व्यंजक जिसमें दो पद होते हैं, द्विपद कहलाता है। उदाहरण: x ² + y ² , x + 2
त्रिपद: एक बीजगणितीय व्यंजक जिसमें तीन पद होते हैं, त्रिपद कहलाता है। उदाहरण: x ² + y ² + z ² , x +y +2

गुणक

प्रत्येक मात्रा (स्थिर या शाब्दिक) को एक उत्पाद बनाने के लिए गुणा किया जाता है, जिसे उत्पाद का कारक कहा जाता है और किसी उत्पाद में किसी भी कारक को शेष कारकों के उत्पाद का गुणांक कहा जाता है। पद में, अभिव्यक्ति 5p ³ − 11p ² q + 7 का -11p ² q,

• संख्यात्मक गुणांक -11 है।
• शाब्दिक गुणांक p ² q है।
• p ² का गुणांक -11q है।
• ^-11p2 का गुणांक q है।
  

पसंद और विपरीत शर्तें

बीजगणितीय व्यंजक के पद जिनमें समान चर (ओं) और चरों के समान घातांक होते हैं, समान पद कहलाते हैं। समान पद केवल गुणांकों में भिन्न हो सकते हैं।
2xy+ 3x + 4y + 5xy + 7y
पद 2xy और 5xy समान पद हैं। 4y और 7y समान पद हैं।

बीजगणितीय व्यंजक 2x + 3xy + 5y में सभी पद असमान हैं।

बहुपद

एक बीजगणितीय अभिव्यक्ति जिसमें शामिल चर की शक्तियां गैर-नकारात्मक पूर्णांक हैं, बहुपद कहलाती हैं।

\(x^3+ x^2 + 2x + 1\) एक चर x में एक बहुपद है।
\(6x - \frac{4x}{y} + 2y + 3 \) बहुपद नहीं है (ध्यान दें कि दूसरे पद में y की घात -1 है)

समान शर्तों का जोड़ और घटाव

जोड़ या घटाकर समान पदों को संयोजित करने के लिए, दिए गए पदों के संख्यात्मक गुणांकों को बस जोड़ें या घटाएँ।
उदाहरण:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

बीजगणितीय व्यंजकों का जोड़ और घटाव

बीजगणितीय व्यंजक जोड़ने के लिए, बस उनके समान पदों को जोड़ें। सुविधा के लिए एक ही कॉलम में एक के नीचे एक समान शब्द लिखें। उदाहरण:
जोड़ना -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) , \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

घटाव के लिए, व्यंजक के प्रत्येक पद के चिह्न को पलटें जिसे घटाया जा रहा है और फिर दोनों व्यंजकों को एक साथ जोड़ दें। उदाहरण
\(3x^2 + 5x + 7y^2\) को \(9x^2 + 7x + 5y + 10y^2\) से घटाएं

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

आप ग्रुपिंग का उपयोग करके बीजगणितीय व्यंजकों को जोड़ या घटा भी सकते हैं। आइए उपरोक्त उदाहरण लें और ग्रुपिंग का उपयोग करके घटाएं:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

बीजगणितीय व्यंजकों का गुणन

बीजगणितीय व्यंजकों के गुणन को तीन स्थितियों में विभाजित किया जा सकता है, आइए उन पर अलग से चर्चा करें:

मामला मैं (एकपद का गुणन) : सामान्य चरों के घातांकों को जोड़कर, असामान्य चरों को अपरिवर्तित छोड़ते हुए, उनके संख्यात्मक गुणांकों को आपस में और फिर चरों का गुणा करें। उदाहरण: 6bc और 5b = का गुणनफल ज्ञात कीजिए \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

मामला द्वितीय (एक एकपदी द्वारा गुणन बहुपद) : बहुपद के प्रत्येक पद को एकपदी से गुणा कीजिए। उदाहरण: ^3xy और x2 + ^2xy + y2 का गुणनफल है
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

मामला तृतीय (बहुपद द्वारा बहुपद का गुणन) : एक बहुपद के प्रत्येक पद को दूसरे के प्रत्येक पद से गुणा करें और फिर गुणनफल को सरल बनाने के लिए समान पदों को संयोजित करें। उदाहरण: (2x + 3y) और (x + y + 2) का गुणनफल है
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

बीजीय व्यंजकों का विभाजन

बीजगणितीय व्यंजक के विभाजन को नीचे तीन स्थितियों का उपयोग करके समझाया जा सकता है।

मामला मैं (एकपदी को एकपदी द्वारा विभाजित करना) : एकपदी को एकपदी से विभाजित करने के लिए, सामान्य चरों के घातांकों को घटाकर उनके संख्यात्मक गुणांकों का भागफल और चरों का भागफल ज्ञात करें। उदाहरण:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

मामला द्वितीय (एकपदी द्वारा बहुपद का विभाजन) : बहुपद के प्रत्येक पद को एक एकपदी से विभाजित करें और फिर उपरोक्त मामले में दिए गए अनुसार विभाजित करें। उदाहरण:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

मामला तृतीय ( एक बहुपद द्वारा एक बहुपद का विभाजन ): यह दीर्घ विभाजन विधि द्वारा किया जाएगा। आइए इसे एक उदाहरण की मदद से समझने की कोशिश करते हैं।
\(8x^2 + 9x - 8 \div 8x + 1\)

भागफल (x) का पहला पद ज्ञात करने के लिए भाज्य के पहले पद (8x ² ) को भाजक के पहले पद (8x) से विभाजित करके प्रारंभ करें और फिर भागफल पद को भाजक से गुणा करें और घटाएँ।

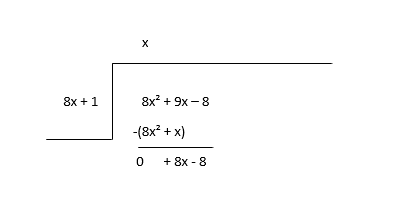
शेषफल को नया लाभांश मानें और भागफल के अगले पद का अनुमान लगाएं।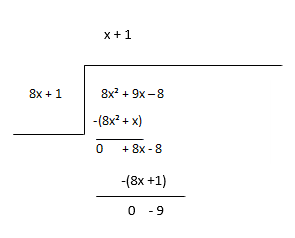

भागफल - x + 1, शेषफल - -9

कोष्ठकों को हटाना और संचालन नियम के आदेश का उपयोग

कोष्ठक वाली बीजगणितीय अभिव्यक्ति को सरल बनाने के लिए, कोष्ठक को इस क्रम में हटा दें:

उदाहरण:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)