Back to the topics list

algebarski izraz

Sadržaj:

• Što je varijabla?
• Vrste algebarskih izraza.
• Koeficijent.
• Uvjeti sviđanja i nesviđanja.
• Polinom.
• Zbrajanje, oduzimanje, množenje i dijeljenje algebarskih izraza.
• Primjena pravila Redoslijed operacija za pojednostavljenje algebarskih izraza.

Doslovni brojevi

U algebri koristimo englesku ili grčku abecedu kao što su a, b, x, y, β, Φ, ... za predstavljanje brojeva. Ova slova se koriste za predstavljanje nepoznatih veličina. Budući da slova predstavljaju brojeve, nazivaju se doslovni brojevi. Doslovni broj može poprimiti bilo koju vrijednost stoga ga nazivamo varijablom . Broj s određenom vrijednošću naziva se konstanta.

Algebarski izraz

Kombinacija konstanti i literala (varijabli) povezanih jednom ili više aritmetičkih operacija (zbrajanje, množenje, oduzimanje, dijeljenje) naziva se algebarski izraz. Jedan ili više znakova (+, −) rastavljaju algebarski izraz na nekoliko dijelova. Svaki dio sa svojim znakom naziva se članom algebarskog izraza. Termin može biti konstanta kao na primjer 4, varijabla, na primjer, x, produkt konstante i varijable, na primjer, 4x ili produkt dviju ili više varijabli, na primjer, xy, xy ² .

Monomal: Algebarski izraz koji ima samo jedan član naziva se monom. Primjer: 7x, ab ² , 8
Binom: Algebarski izraz koji ima dva člana naziva se binom. Primjer: x ² + y ² , x + 2
Trinom: Algebarski izraz koji ima tri člana naziva se trinom. Primjer: x ² + y ² + z ² , x + y +2

Koeficijent

Svaka od veličina (konstanta ili literala) pomnožena da se dobije umnožak naziva se faktor umnoška, a bilo koji faktor u umnošku naziva se koeficijent umnoška preostalih faktora. U članu, -11p ² q izraza 5p ³ − 11p ² q + 7,

• Brojčani koeficijent je -11.
• Literalni koeficijent je p ² q.
• Koeficijent p ² je -11q.
• Koeficijent od -11p ² je q.
  

Uvjeti sviđanja i nesviđanja

Za članove algebarskog izraza koji imaju istu varijablu(e) i isti eksponent(e) varijabli kaže se da su slični termini. Slični izraz se može razlikovati samo u koeficijentima.
2xy+ 3x + 4y + 5xy + 7y
Termini 2xy i 5xy su slični terminima. 4y i 7y su kao pojmovi.

Svi članovi u algebarskom izrazu 2x + 3xy + 5y su različiti.

Polinom

Algebarski izraz u kojem su potencije uključenih varijabli nenegativni cijeli brojevi naziva se polinom.

\(x^3+ x^2 + 2x + 1\) je polinom u jednoj varijabli x.
\(6x - \frac{4x}{y} + 2y + 3 \) nije polinom (primijetite da y u drugom članu ima potenciju -1)

Zbrajanje i oduzimanje sličnih članova

Za kombiniranje sličnih izraza zbrajanjem ili oduzimanjem, jednostavno dodajte ili oduzmite numeričke koeficijente zadanih izraza.
Primjer:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

Zbrajanje i oduzimanje algebarskih izraza

Da biste dodali algebarski izraz, jednostavno dodajte njihove slične izraze. Radi lakšeg snalaženja, napišite slične pojmove jedan ispod drugog u istom stupcu. Primjer:
Dodati -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) , \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

Za oduzimanje , okrenite znak svakog člana izraza koji se oduzima i zatim zbrojite ta dva izraza. Primjer
Oduzmi \(3x^2 + 5x + 7y^2\) od \(9x^2 + 7x + 5y + 10y^2\)

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

Također možete dodavati ili oduzimati algebarske izraze pomoću grupiranja. Uzmimo gornji primjer i oduzmimo pomoću grupiranja:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

Množenje algebarskih izraza

Množenje algebarskog izraza može se podijeliti u tri slučaja, raspravimo ih zasebno:

Slučaj ja (Množenje monoma) : Pomnožite njihove numeričke koeficijente zajedno, a zatim varijable dodavanjem eksponenata zajedničkih varijabli, ostavljajući neuobičajene varijable nepromijenjene. Primjer: Pronađite umnožak 6bc i 5b = \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

Slučaj II (Množenje polinoma monomom) : Pomnožite svaki član polinoma monomom. Primjer: umnožak 3xy i x ² + 2xy + y ² je
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

Slučaj III (Množenje polinoma polinomom) : Pomnožite svaki član jednog polinoma sa svakim članom drugog i zatim kombinirajte slične članove da biste pojednostavili proizvod. Primjer: umnožak (2x + 3y) i (x + y + 2) je
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

Podjela algebarskih izraza

Podjela algebarskog izraza može se objasniti korištenjem tri slučaja.

Slučaj ja (Dijeljenje monoma s monomom) : Da biste podijelili monom s monomom, pronađite kvocijente njihovih numeričkih koeficijenata i kvocijente varijabli oduzimanjem eksponenata zajedničkih varijabli. Primjer:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

Slučaj II (Dijeljenje polinoma monomom) : Podijelite svaki član polinoma monomom, a zatim podijelite kao što je navedeno u gornjem slučaju. Primjer:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

Slučaj III ( Dijeljenje polinoma polinomom ): Ovo će biti učinjeno metodom dugog dijeljenja. Pokušajmo ovo razumjeti pomoću primjera.
\(8x^2 + 9x - 8 \div 8x + 1\)

Započnite dijeljenjem prvog člana djelitelja (8x ² ) s prvim članom djelitelja (8x) da biste pronašli prvi član kvocijenta (x), a zatim pomnožite kvocijent s djeliteljem i oduzmite.

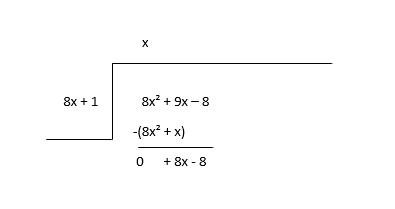
Ostatak smatrajte novom dividendom i procijenite sljedeći izraz kvocijenta.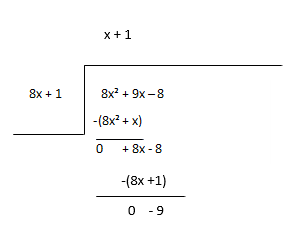

Kvocijent - x + 1, Ostatak - -9

Uklanjanje zagrada i korištenje pravila Redoslijed operacija

Da biste pojednostavili algebarski izraz koji sadrži zagrade, uklonite zagrade redoslijedom:

Primjer:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)