Back to the topics list

ekspresi aljabar

Isi:

• Apa itu Variabel?
• Jenis Ekspresi Aljabar.
• Koefisien.
• Ketentuan Suka dan Tidak Suka.
• Polinomial.
• Penambahan, Pengurangan, Perkalian dan Pembagian ekspresi Aljabar.
• Penerapan aturan Urutan Operasi untuk menyederhanakan ekspresi Aljabar.

Angka Literal

Dalam Aljabar kami menggunakan Abjad Inggris atau Yunani seperti a, b, x, y, β, Φ, ... untuk mewakili angka. Huruf-huruf ini digunakan untuk mewakili jumlah yang tidak diketahui. Karena huruf mewakili angka maka disebut angka literal. Angka literal dapat mengasumsikan nilai apa pun, oleh karena itu kami menyebutnya variabel . Bilangan yang nilainya pasti disebut konstanta.

Ekspresi aljabar

Kombinasi konstanta dan literal (variabel) yang dihubungkan oleh satu atau lebih operasi aritmatika (penjumlahan, perkalian, pengurangan, pembagian) disebut ekspresi aljabar. Satu atau lebih tanda (+, −) memecah ekspresi aljabar menjadi beberapa bagian. Setiap bagian dengan tandanya disebut istilah ekspresi aljabar. Suatu suku dapat berupa konstanta seperti misalnya 4, variabel, misalnya x, hasil kali konstanta dan variabel, misalnya 4x, atau hasil kali dua variabel atau lebih, misalnya xy, xy ² .

Monomial: Ekspresi aljabar yang hanya memiliki satu istilah disebut monomial. Contoh: 7x, ab ² , 8
Binomial: Ekspresi aljabar yang memiliki dua suku disebut binomial. Contoh: x ² + y ² , x + 2
Trinomial: Ekspresi aljabar yang memiliki tiga suku disebut trinomial. Contoh: x ² + y ² + z ² , x +y +2

Koefisien

Setiap kuantitas (konstanta atau literal) dikalikan untuk membentuk produk, disebut faktor produk dan setiap faktor dalam produk disebut koefisien produk dari faktor yang tersisa. Dalam istilah, -11p ² q dari ekspresi 5p ³ − 11p ² q + 7,

• Koefisien numerik adalah -11.
• Koefisien literal adalah p ² q.
• Koefisien p ² adalah -11q.
• Koefisien -11p ² adalah q.
  

Ketentuan Suka dan Tidak Suka

Suku-suku dari ekspresi aljabar yang memiliki variabel yang sama dan eksponen yang sama dari variabel-variabel tersebut dikatakan suku-suku sejenis. Istilah serupa hanya dapat berbeda dalam koefisien.
2xy+ 3x + 4y + 5xy + 7y
Suku 2xy dan 5xy adalah suku sejenis. 4y dan 7y adalah suku-suku sejenis.

Suku-suku dalam ekspresi aljabar 2x + 3xy + 5y semuanya tidak sama.

Polinomial

Ekspresi aljabar di mana kekuatan variabel yang terlibat adalah bilangan bulat non-negatif disebut polinomial.

\(x^3+ x^2 + 2x + 1\) adalah polinomial dalam satu variabel x.
\(6x - \frac{4x}{y} + 2y + 3 \) bukan polinomial (perhatikan bahwa y pada suku kedua memiliki pangkat -1)

Penjumlahan dan Pengurangan Suku-Suku Sejenis

Untuk menggabungkan suku-suku sejenis dengan penjumlahan atau pengurangan, cukup tambahkan atau kurangi koefisien numerik dari suku-suku yang diberikan.
Contoh:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

Penambahan dan Pengurangan Ekspresi Aljabar

Untuk menjumlahkan ekspresi aljabar, cukup tambahkan suku-suku sejenisnya. Untuk kenyamanan, tulis istilah yang mirip satu di bawah yang lain di kolom yang sama. Contoh:
Menambahkan -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) , \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

Untuk pengurangan , balikkan tanda setiap suku dari pernyataan yang dikurangi, lalu jumlahkan kedua pernyataan tersebut. Contoh
Kurangi \(3x^2 + 5x + 7y^2\) dari \(9x^2 + 7x + 5y + 10y^2\)

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

Anda juga dapat menambah atau mengurangi ekspresi aljabar menggunakan Pengelompokan. Mari kita ambil contoh di atas dan kurangi menggunakan Pengelompokan:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

Perkalian Ekspresi Aljabar

Perkalian ekspresi aljabar dapat dibagi menjadi tiga kasus, mari kita bahas secara terpisah:

Kasus SAYA (Perkalian Monomial) : Kalikan koefisien numeriknya bersama-sama dan kemudian variabel dengan menjumlahkan eksponen dari variabel yang sama, biarkan variabel yang tidak biasa tidak berubah. Contoh: Temukan produk dari 6bc dan 5b = \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

Kasus II (Perkalian Polinomial dengan Monomial) : Kalikan setiap suku polinomial dengan monomial. Contoh: Produk dari 3xy dan x ² + 2xy + y ² adalah
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

Kasus AKU AKU AKU (Perkalian Polinomial dengan Polinomial) : Kalikan setiap suku dari satu polinomial dengan setiap suku polinomial lainnya, lalu gabungkan suku-suku yang serupa untuk menyederhanakan hasilnya. Contoh: Produk dari (2x + 3y) dan (x + y + 2) adalah
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

Pembagian Ekspresi Aljabar

Pembagian ekspresi aljabar dapat dijelaskan dengan menggunakan tiga kasus di bawah ini.

Kasus SAYA (Pembagian Monomial dengan Monomial) : Untuk membagi monomial dengan monomial, carilah hasil bagi dari koefisien numeriknya dan hasil bagi variabelnya dengan mengurangkan eksponen dari variabel yang sama. Contoh:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

Kasus II (Pembagian Polinomial dengan Monomial) : Bagilah setiap suku polinomial dengan monomial dan kemudian bagi seperti yang diberikan dalam kasus di atas. Contoh:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

Kasus AKU AKU AKU ( Pembagian Polinomial dengan Polinomial ): Ini akan dilakukan dengan metode pembagian panjang. Mari kita coba memahami ini menggunakan contoh.
\(8x^2 + 9x - 8 \div 8x + 1\)

Mulailah dengan membagi suku pertama dari pembagi(8x ² ) dengan suku pertama pembagi(8x) untuk menemukan suku pertama hasil bagi(x) lalu kalikan suku hasil bagi dengan pembagi dan kurangi.

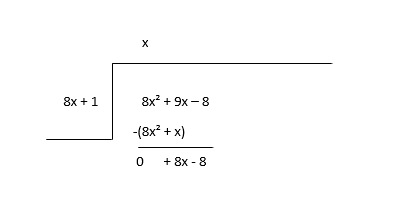
Pertimbangkan sisanya sebagai dividen baru dan perkirakan suku hasil bagi berikutnya.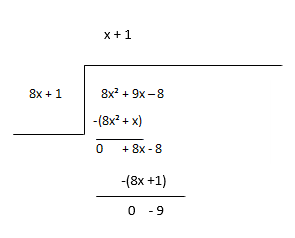

Bagi - x + 1, Sisa - -9

Penghapusan Tanda Kurung dan penggunaan Aturan Urutan Operasi

Untuk menyederhanakan ekspresi aljabar yang mengandung tanda kurung, hilangkan tanda kurung dengan urutan :

Contoh:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)