Back to the topics list

espressione algebrica

Contenuti:

• Cos'è una variabile?
• Tipi di espressione algebrica.
• Coefficiente.
• Termini simili e dissimili.
• Polinomio.
• Addizione, sottrazione, moltiplicazione e divisione di espressioni algebriche.
• Applicazione della regola dell'ordine delle operazioni per semplificare l'espressione algebrica.

Numeri letterali

In Algebra usiamo alfabeti inglesi o greci come a, b, x, y, β, Φ, ... per rappresentare i numeri. Queste lettere sono usate per rappresentare quantità sconosciute. Poiché le lettere rappresentano i numeri, vengono chiamate numeri letterali. Un numero letterale può assumere qualsiasi valore quindi lo chiamiamo variabile . Un numero con un valore definito è chiamato costante.

Espressione algebrica

Una combinazione di costanti e letterali (variabili) collegati da una o più operazioni aritmetiche (addizione, moltiplicazione, sottrazione, divisione) è chiamata espressione algebrica. Uno o più segni (+, −) spezzano un'espressione algebrica in più parti. Ogni parte con il suo segno è chiamata termine dell'espressione algebrica. Un termine può essere una costante come ad esempio 4, una variabile, ad esempio x, un prodotto di una costante e una variabile, ad esempio 4x o un prodotto di due o più variabili, ad esempio xy, xy ² .

Monomial: un'espressione algebrica che ha un solo termine è chiamata monomial. Esempio: 7x, ab ² , 8
Binomiale: un'espressione algebrica che ha due termini è chiamata binomiale. Esempio: x ² + y ² , x + 2
Trinomio: un'espressione algebrica che ha tre termini è chiamata trinomio. Esempio: x ² + y ² + z ² , x + y +2

Coefficiente

Ciascuna delle quantità (costanti o letterali) moltiplicate per formare un prodotto, è chiamata fattore del prodotto e qualsiasi fattore in un prodotto è chiamato coefficiente del prodotto dei restanti fattori. Nel termine, -11p ² q dell'espressione 5p ³ − 11p ² q + 7,

• Il coefficiente numerico è -11.
• Il coefficiente letterale è p ² q.
• Il coefficiente di p ² è -11q.
• Il coefficiente di -11p ² è q.
  

Termini simili e dissimili

I termini dell'espressione algebrica aventi la stessa variabile(i) e lo stesso(i) esponente(i) delle variabili sono detti termini simili. Come termine può differire solo in coefficienti.
2xy+ 3x + 4y + 5xy + 7y
I termini 2xy e 5xy sono termini simili. 4y e 7y sono termini simili.

I termini nell'espressione algebrica 2x + 3xy + 5y sono tutti diversi.

Polinomio

Un'espressione algebrica in cui le potenze delle variabili coinvolte sono numeri interi non negativi è chiamata polinomio.

\(x^3+ x^2 + 2x + 1\) è un polinomio in una variabile x.
\(6x - \frac{4x}{y} + 2y + 3 \) non è un polinomio (si noti che y nel secondo termine ha potenza -1)

Addizione e sottrazione di termini simili

Per combinare termini simili per addizione o sottrazione, è sufficiente aggiungere o sottrarre i coefficienti numerici dei termini dati.
Esempio:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

Addizione e sottrazione di espressioni algebriche

Per aggiungere un'espressione algebrica, aggiungi semplicemente i loro termini simili. Per comodità scrivi i termini simili uno sotto l'altro nella stessa colonna. Esempio:
Aggiungere -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) , \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

Per sottrazione , capovolgi il segno di ogni termine dell'espressione che viene sottratta e quindi somma le due espressioni insieme. Esempio
Sottrai \(3x^2 + 5x + 7y^2\) da \(9x^2 + 7x + 5y + 10y^2\)

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

Puoi anche aggiungere o sottrarre espressioni algebriche utilizzando Raggruppamento. Prendiamo l'esempio sopra e sottraiamo usando Raggruppamento:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

Moltiplicazione di espressioni algebriche

La moltiplicazione dell'espressione algebrica può essere suddivisa in tre casi, discutiamoli separatamente:

Caso io (Moltiplicazione di Monomi) : Moltiplicare i loro coefficienti numerici insieme e poi le variabili sommando gli esponenti delle variabili comuni, lasciando invariate le variabili non comuni. Esempio: trova il prodotto di 6bc e 5b = \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

Caso II (Moltiplicazione di un polinomio per un monomio) : Moltiplica ogni termine del polinomio per il monomio. Esempio: prodotto di 3xy e x ² + 2xy + y ² is
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

Caso III (Moltiplicazione di un polinomio per polinomio) : Moltiplica ogni termine di un polinomio per ogni termine dell'altro e poi combina i termini simili per semplificare il prodotto. Esempio: il prodotto di (2x + 3y) e (x + y + 2) è
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

Divisione di espressioni algebriche

La divisione dell'espressione algebrica può essere spiegata utilizzando i tre casi seguenti.

Caso io (Divisione di un monomio per un monomio) : per dividere un monomio per un monomio, trovare i quozienti dei loro coefficienti numerici e i quozienti delle variabili sottraendo gli esponenti delle variabili comuni.Esempio:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

Caso II (Division of Polynomial by Monomial) : Dividi ogni termine del polinomio per un monomio e poi dividi come indicato nel caso precedente. Esempio:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

Caso III ( Divisione di un polinomio per un polinomio ): Questo sarà fatto con il metodo della divisione lunga. Proviamo a capirlo con un esempio.
\(8x^2 + 9x - 8 \div 8x + 1\)

Inizia dividendo il primo termine del dividendo(8x ² ) con il primo termine del divisore(8x) per trovare il primo termine del quoziente(x) e poi moltiplichi il termine del quoziente per il divisore e sottrai.

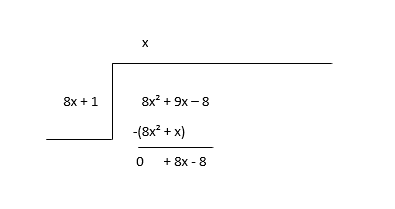
Considera il resto come il nuovo dividendo e stima il termine successivo del quoziente.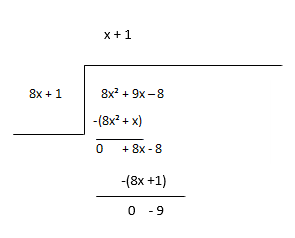

Quoziente - x + 1, Resto - -9

Rimozione delle parentesi e utilizzo della regola dell'ordine delle operazioni

Per semplificare un'espressione algebrica contenente parentesi, rimuovere le parentesi nell'ordine di:

Esempio:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)