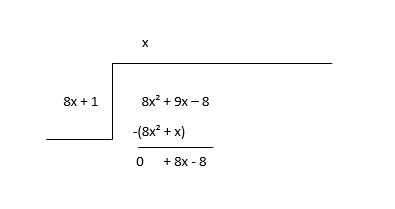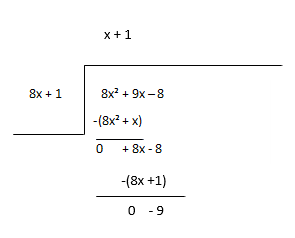コンテンツ:
- 変数とは
- 代数式の種類。
- 係数。
- 好きな言葉と違う言葉。
- 多項式。
- 代数式の足し算、引き算、掛け算、割り算。
- 代数式を単純化するための演算順序規則の適用。
リテラル数
代数では、a、b、x、y、β、Φなどの英語またはギリシャ語のアルファベットを使用して数値を表します。これらの文字は、未知の量を表すために使用されます。文字は数字を表すため、文字通りの数字と呼ばれます。リテラル数値は任意の値をとることができるため、変数と呼びます。値が決まっている数を定数と呼びます。
代数式
定数とリテラル(変数)を1つ以上の算術演算(足し算、掛け算、引き算、割り算)でつなげたものを代数式と呼びます。 1 つまたは複数の記号 (+、−) は、代数式をいくつかの部分に分割します。符号を付けた各部分を代数式の項と呼びます。項は、たとえば 4 のような定数、たとえば x などの変数、たとえば 4x などの定数と変数の積、または xy、xy 2などの 2 つ以上の変数の積である場合があります。
単項式:項が 1 つしかない代数式を単項式と呼びます。例: 7x、ab 2 、8
二項: 2 つの項を持つ代数式は、二項と呼ばれます。例: x 2 + y 2 , x + 2
三項式: 3 つの項を持つ代数式は、三項式と呼ばれます。例: x 2 + y 2 + z 2 、 x +y +2
係数
積を形成するために乗算される各量 (定数またはリテラル) は、積の係数と呼ばれ、積の任意の係数は、残りの係数の積の係数と呼ばれます。式5p 3 − 11p 2 q + 7の-11p 2 qの項では、
- 数値係数は-11です。
- リテラル係数は p 2 q です。
- p 2の係数は -11q です。
- -11p 2の係数は q です。
好きな言葉と違う言葉
同じ変数と変数の同じ指数を持つ代数式の項は、類似項であると言われます。同様の項は、係数のみが異なる可能性があります。
2xy+ 3x + 4y + 5xy + 7y
項 2xy と 5xy は類似項です。 4y と 7y は似たような用語です。
代数式 2x + 3xy + 5y の項はすべて異なります。
多項式
関連する変数の累乗が非負の整数である代数式は、多項式と呼ばれます。
\(x^3+ x^2 + 2x + 1\) 1 つの変数 x の多項式です。
\(6x - \frac{4x}{y} + 2y + 3 \)多項式ではありません (第 2 項の y の累乗は -1 であることに注意してください)
同類項の加減
足し算または引き算によって同様の項を組み合わせるには、与えられた項の数値係数を単に足すか引くだけです。
例:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)
代数式の足し算と引き算
代数式を追加するには、単純に類似項を追加します。便宜上、同じ列に同じ用語を下に並べて書きます。例:
追加 -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) , \(x^2\; + 2x + 3xy + 6y + 3y^2\)
\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)
減算の場合、減算される式の各項の符号を反転してから、2 つの式を合計します。例
\(3x^2 + 5x + 7y^2\)から\(9x^2 + 7x + 5y + 10y^2\)を引く
\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)
グループ化を使用して、代数式を加算または減算することもできます。上記の例を取り上げて、Grouping を使用して減算してみましょう。
\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)
代数式の乗算
代数式の乗算は 3 つのケースに分けることができます。個別に説明しましょう。
場合私(単項式の乗算) : それらの数値係数を乗算し、共通変数の指数を追加して変数を乗算し、非共通変数は変更しません。例: 6bc と 5b の積を求める = \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)
場合Ⅱ (単項式による乗算多項式) : 多項式の各項に単項式を乗算します。例: 3xy と x 2 + 2xy + y 2の積は
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)
場合Ⅲ (多項式による多項式の乗算) : 一方の多項式の各項を他方の各項で乗算し、類似の項を組み合わせて積を簡略化します。例: (2x + 3y) と ( x + y + 2) の積は
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)
代数式の除算
代数式の除算は、以下の 3 つのケースを使用して説明できます。
場合私(単項式による単項式の除算) : 単項式を単項式で除算するには、それらの数値係数の商と変数の商を、共通変数の指数を減算して求めます。例:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)
場合Ⅱ (単項式による多項式の除算) : 多項式の各項を単項式で除算し、上記の場合のように除算します。例:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
場合Ⅲ (多項式による多項式の除算): これは、長い除算法によって行われます。例を使ってこれを理解してみましょう。
\(8x^2 + 9x - 8 \div 8x + 1\)
被除数の第 1 項 (8x 2 ) を除数の第 1 項 (8x) で割り、商の第 1 項 (x) を求めてから、商の項に除数を掛けて減算します。
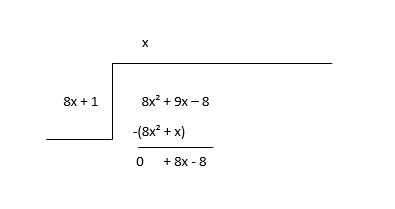
残りを新しい配当と見なし、商の次の項を見積もります。
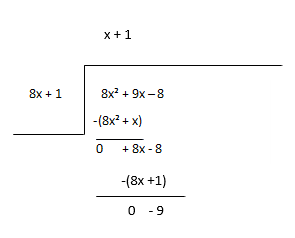
商 - x + 1、剰余 - -9
ブラケットの削除と操作順序ルールの使用
角かっこを含む代数式を単純化するには、次の順序で角かっこを削除します。

例:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)