Back to the topics list

алгебарски израз

Содржина:

• Што е променлива?
• Видови алгебарски изрази.
• Коефициент.
• Услови за лајк и за разлика.
• Полином.
• Собирање, одземање, множење и делење на алгебарски израз.
• Примена на правилото Ред на операции за поедноставување на алгебарскиот израз.

Буквални броеви

Во Алгебра користиме англиски или грчки азбуки како a, b, x, y, β, Φ, ... за да ги претставиме броевите. Овие букви се користат за да претставуваат непознати количини. Бидејќи буквите претставуваат броеви, тие се нарекуваат буквални броеви. Буквален број може да преземе каква било вредност, па затоа го нарекуваме променлива . Бројот со одредена вредност се нарекува константа.

Алгебарски израз

Комбинацијата од константи и литерали (променливи) поврзани со една или повеќе аритметички операции (собирање, множење, одземање, делење) се нарекува алгебарски израз. Еден или повеќе знаци (+, −) разделуваат алгебарски израз на неколку делови. Секој дел со својот знак се нарекува член на алгебарскиот израз. Поимот може да биде константа како на пример 4, променлива, на пример, x, производ на константа и променлива, на пример, 4x или производ од две или повеќе променливи, на пример, xy, xy ² .

Моном: Алгебарскиот израз кој има само еден член се нарекува моном. Пример: 7x, ab ² , 8
Бином: Алгебарскиот израз кој има два члена се нарекува бином. Пример: x ² + y ² , x + 2
Трином: Алгебарскиот израз кој има три члена се нарекува трином. Пример: x ² + y ² + z ² , x +y +2

Коефициент

Секоја од количините (константа или буквални) помножена за да се формира производ, се нарекува фактор на производот, а секој фактор во производот се нарекува коефициент на производот на останатите фактори. Во членот, -11p ² q од изразот 5p ³ − 11p ² q + 7,

• Нумеричкиот коефициент е -11.
• Буквален коефициент е p ² q.
• Коефициентот на p ² е -11q.
• Коефициентот -11p ² е q.
  

Услови за лајк и за разлика

Условите на алгебарскиот израз кои имаат иста променлива(и) и исти експонент(и) на променливите се вели дека се слични поими. Лајковиот термин може да се разликува само во коефициенти.
2xy+ 3x + 4y + 5xy + 7y
Термините 2xy и 5xy се како термини. 4г и 7г се како термини.

Термините во алгебарскиот израз 2x + 3xy + 5y не се слични.

Полином

Алгебарскиот израз во кој моќите на вклучените променливи се ненегативни цели броеви се нарекува полином.

\(x^3+ x^2 + 2x + 1\) е полином во една променлива x.
\(6x - \frac{4x}{y} + 2y + 3 \) не е полином (забележете дека y во вториот член има моќност -1)

Собирање и одземање на поими слични

За да комбинирате слични членови со собирање или одземање, едноставно додадете или одземете ги нумеричките коефициенти на дадените членови.
Пример:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

Собирање и одземање на алгебарски изрази

За да додадете алгебарски израз, едноставно додадете ги нивните како термини. За погодност напишете го сличниот термин еден под друг во истата колона. Пример:
Додај -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) , \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

За одземање , превртете го знакот на секој член од изразот што се одзема и потоа соберете ги двата изрази заедно. Пример
Одземете \(3x^2 + 5x + 7y^2\) од \(9x^2 + 7x + 5y + 10y^2\)

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

Можете исто така да додавате или одземате алгебарски изрази користејќи Групирање. Да го земеме горенаведениот пример и да одземеме користејќи Групирање:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

Множење на алгебарски изрази

Множењето на алгебарскиот израз може да се подели во три случаи, ајде да ги разгледаме одделно:

Случај Јас (Множење на мономи) : множете ги нивните нумерички коефициенти заедно, а потоа променливите со додавање на експонентите на заедничките променливи, оставајќи ги невообичаените променливи непроменети. Пример: Најдете го производот од 6bc и 5b = \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

Случај II (Множење полином со моном) : Помножете го секој член од полиномот со мономот. Пример: Производ од 3xy и x ² + 2xy + y ² е
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

Случај III (Множење на полином со полином) : множете го секој член од еден полином со секој член на другиот и потоа комбинирајте ги сличните членови за да го поедноставите производот. Пример: Производ од (2x + 3y) и ( x + y + 2) е
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

Поделба на алгебарски изрази

Поделбата на алгебарскиот израз може да се објасни користејќи подолу три случаи.

Случај Јас (Поделба на моном со моном) : За да се подели моном со моном, пронајдете ги количниците на нивните нумерички коефициенти и количниците на променливите со одземање на експонентите на заедничките променливи. Пример:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

Случај II (Поделба на полиномот со моном) : Поделете го секој член од полиномот со моном и потоа поделете го како што е дадено во горниот случај. Пример:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

Случај III ( Поделба на полином со полином ): Ова ќе се направи со методот на долга поделба. Ајде да се обидеме да го разбереме ова користејќи пример.
\(8x^2 + 9x - 8 \div 8x + 1\)

Започнете со делење на првиот член од дивидендата(8x2 ⁾ со првиот член на делителот(8x) за да го најдете првиот член од количникот(x), а потоа го множите членот на количникот со делителот и одземате.

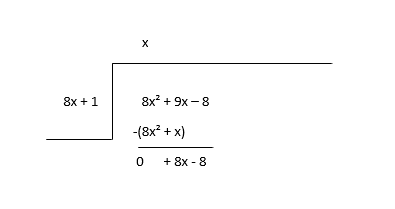
Размислете за остатокот како нова дивиденда и проценете го следниот член на количникот.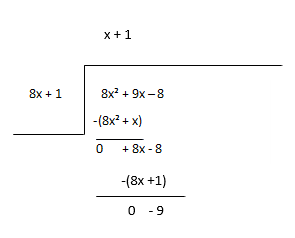

Количина - x + 1, Остаток - -9

Отстранување на загради и употреба на Правило за редослед на операции

За да се поедностави алгебарскиот израз кој содржи загради, отстранете ги заградите по редослед:

Пример:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)