Back to the topics list

алгебрийн илэрхийлэл

Агуулга:

• Хувьсагч гэж юу вэ?
• Алгебрийн илэрхийлэлийн төрлүүд.
• Коэффицент.
• Таалагдсан болон таалагдаагүй нөхцөл.
• Олон гишүүнт.
• Алгебрийн илэрхийлэлийг нэмэх, хасах, үржүүлэх, хуваах.
• Алгебрийн илэрхийллийг хялбарчлахын тулд үйлдлийн дарааллын дүрмийг ашиглах.

Литерал тоо

Алгебрийн хичээлд бид тоонуудыг илэрхийлэхийн тулд a, b, x, y, β, Φ, ... зэрэг англи эсвэл грек цагаан толгойн үсгүүдийг ашигладаг. Эдгээр үсэг нь үл мэдэгдэх хэмжигдэхүүнийг илэрхийлэхэд хэрэглэгддэг. Үсгүүд нь тоог илэрхийлдэг тул тэдгээрийг шууд тоо гэж нэрлэдэг. Шууд утга нь ямар ч утгыг авч чаддаг тул бид үүнийг хувьсагч гэж нэрлэдэг. Тодорхой утгатай тоог тогтмол гэж нэрлэдэг.

Алгебрийн илэрхийлэл

Нэг буюу хэд хэдэн арифметик үйлдлээр (нэмэх, үржүүлэх, хасах, хуваах) холбогдсон тогтмол ба литералуудын (хувьсагч) хослолыг алгебрийн илэрхийлэл гэж нэрлэдэг. Нэг буюу хэд хэдэн тэмдэг (+, −) нь алгебр илэрхийллийг хэд хэдэн хэсэгт хуваадаг. Тэмдэгтэй хэсэг бүрийг алгебр илэрхийллийн гишүүн гэж нэрлэдэг . Нэр томьёо нь жишээлбэл 4, хувьсагч, жишээлбэл, x, тогтмол ба хувьсагчийн үржвэр, жишээлбэл, 4x эсвэл хоёр ба түүнээс дээш хувьсагчийн үржвэр, жишээлбэл, xy, xy ² байж болно.

Мономиал: Ганц гишүүнтэй алгебрийн илэрхийллийг мономиал гэнэ. Жишээ нь: 7x, ab ² , 8
Хоёр гишүүн : Хоёр гишүүнтэй алгебрийн илэрхийлэлийг бином гэнэ. Жишээ нь: x ² + y ² , x + 2
Гурвалсан гишүүн: Гурван гишүүнтэй алгебрийн илэрхийллийг гурвалсан гишүүн гэнэ. Жишээ нь: x ² + y ² + z ² , x +y +2

Коэффицент

Бүтээгдэхүүн үүсгэхийн тулд үржүүлсэн тоо хэмжээ (тогтмол эсвэл литерал) бүрийг бүтээгдэхүүний хүчин зүйл гэж нэрлэдэг бөгөөд бүтээгдэхүүний аливаа хүчин зүйлийг үлдсэн хүчин зүйлсийн бүтээгдэхүүний коэффициент гэж нэрлэдэг. Нэр томьёогоор 5p ³ − 11p ² q + 7 илэрхийллийн -11p ² q,

• Тоон коэффициент -11.
• Литерал коэффициент нь p ² q байна.
• p ² коэффициент нь -11q байна.
• -11p ² коэффициент нь q байна.
  

Таалагдсан болон таалагдаагүй нөхцөл

Ижил хувьсагч(ууд) ба хувьсагчдын ижил илтгэгч(үүд)тэй алгебрийн илэрхийллийн гишүүнчлэлийн гишүүдийг нэр томъёотой адил гэнэ. Үүнтэй адил нэр томъёо нь зөвхөн коэффициентээр ялгаатай байж болно.
2xy+ 3x + 4y + 5xy + 7y
2xy ба 5xy нэр томъёо нь нэр томъёотой адил юм. 4y ба 7y нь ижил нөхцөл юм.

2x + 3xy + 5y алгебрийн илэрхийлэл дэх нэр томъёо нь бүгд адилгүй.

Олон гишүүнт

Оролцсон хувьсагчдын зэрэглэл нь сөрөг бус бүхэл тоо байх алгебрийн илэрхийллийг олон гишүүнт гэж нэрлэдэг.

\(x^3+ x^2 + 2x + 1\) нь нэг x хувьсагчийн олон гишүүнт юм.
\(6x - \frac{4x}{y} + 2y + 3 \) нь олон гишүүнт биш (хоёр дахь гишүүний y нь -1 чадалтай болохыг анхаарна уу)

Like нэр томъёоны нэмэх, хасах

Ижил нэр томъёог нэмэх, хасах замаар нэгтгэхийн тулд өгөгдсөн нөхцлийн тоон коэффициентийг нэмэх буюу хасахад л хангалттай.
Жишээ:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

Алгебрийн илэрхийлэлийн нэмэх ба хасах

Алгебрийн илэрхийлэл нэмэхийн тулд зүгээр л тэдний адил нөхцөлийг нэмнэ үү. Тохиромжтой болгохын тулд ижил багананд ижил нэр томъёог нэг дор бичнэ үү. Жишээ:
Нэмэх -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) , \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

Хасах үйлдлийг хийхийн тулд хасагдаж буй илэрхийллийн гишүүн бүрийн тэмдгийг эргүүлж, дараа нь хоёр илэрхийллийг нэгтгэнэ. Жишээ
\(9x^2 + 7x + 5y + 10y^2\) )-аас \ \(3x^2 + 5x + 7y^2\) .

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

Та мөн Бүлэглэх аргыг ашиглан алгебрийн илэрхийлэл нэмэх, хасах боломжтой. Дээрх жишээг аваад Бүлэглэх аргыг ашиглан хасъя:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

Алгебр илэрхийллийн үржвэр

Алгебрийн илэрхийлэлийг үржүүлэх нь гурван тохиолдолд хуваагдаж болох тул тэдгээрийг тусад нь авч үзье.

Кейс I (Мономичийн үржвэр) : Тэдний тоон коэффициентийг хамтад нь үржүүлж, дараа нь нийтлэг хувьсагчийн илтгэгчийг нэмж хувьсагчдыг үржүүлж, нийтлэг бус хувьсагчдыг хэвээр үлдээнэ. Жишээ: 6bc ба 5b =-ийн үржвэрийг ол \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

Кейс II (Полон гишүүнийг нэг гишүүнээр үржүүлэх) : Олон гишүүнтийн гишүүн бүрийг нэг гишүүнээр үржүүлнэ . Жишээ: 3xy ба x ² + 2xy + y ^2- ийн үржвэр
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

Кейс III (Олон гишүүнийг олон гишүүнтээр үржүүлэх) : Нэг олон гишүүнт гишүүн бүрийг нөгөө гишүүний гишүүн бүрээр үржүүлээд дараа нь ижил төстэй нөхцлүүдийг нэгтгэн үржвэрийг хялбаршуулна. Жишээ нь: (2x + 3y) ба ( x + y + 2) үржвэр
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

Алгебрийн илэрхийлэлийн хэлтэс

Алгебр илэрхийллийн хуваагдлыг доорх гурван тохиолдлыг ашиглан тайлбарлаж болно.

Кейс I (Цан гишүүнийг мономиалаар хуваах) : Мономитийг мономицид хуваахын тулд нийтлэг хувьсагчийн илтгэгчийг хасах замаар тэдгээрийн тоон коэффициентийн хуваалт болон хувьсагчдын категорийг ол.Жишээ:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

Кейс II (Олон гишүүнийг нэг гишүүнд хуваах) : Олон гишүүнт гишүүн бүрийг нэг гишүүнд хувааж, дараа нь дээрх тохиолдолд өгөгдсөнөөр хуваана.Жишээ нь:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

Кейс III ( Олон гишүүнийг олон гишүүнээр хуваах): Үүнийг урт хуваах аргаар хийнэ. Үүнийг жишээгээр ойлгохыг хичээцгээе.
\(8x^2 + 9x - 8 \div 8x + 1\)

Ногдол ашгийн эхний гишүүнийг (8х ² ) хуваагчийн эхний гишүүнд (8х) хувааж эхлээд (x) хэсгийн эхний гишүүнийг олоод дараа нь хуваагчтай үржүүлж хасна.

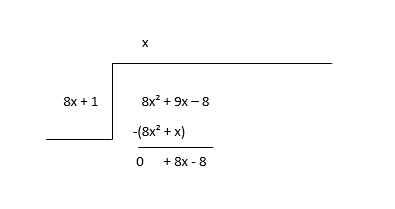
Үлдсэн хэсгийг шинэ ногдол ашиг гэж үзээд хэсгийн дараагийн хугацааг тооцоол.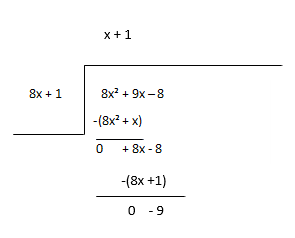

Хэмжээ - x + 1, үлдэгдэл - -9

Хаалтуудыг арилгах, үйл ажиллагааны дарааллын дүрмийг ашиглах

Хаалт агуулсан алгебр илэрхийллийг хялбарчлахын тулд дараах дарааллаар хаалтуудыг арилга.

Жишээ:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)