Back to the topics list

အက္ခရာသင်္ချာ

အကြောင်းအရာများ-

• Variable ဆိုတာ ဘာလဲ။
• Algebraic Expression အမျိုးအစားများ။
• ကိန်းဂဏန်း။
• စည်းမျဥ်းများ နှင့် မတူပါ။
• Polynomial
• အက္ခရာသင်္ချာအသုံးအနှုန်း ပေါင်းထည့်ခြင်း၊ နုတ်ခြင်း၊ မြှောက်ခြင်းနှင့် ပိုင်းခြင်း
• အက္ခရာသင်္ချာအသုံးအနှုန်းကို ရိုးရှင်းစေရန် အစီအစဥ်လုပ်ဆောင်မှုစည်းမျဉ်းကို အသုံးပြုခြင်း။

ပကတိနံပါတ်များ

အက္ခရာသင်္ချာတွင် ကျွန်ုပ်တို့သည် ဂဏန်းများကိုကိုယ်စားပြုရန် a, b, x, y, β, Φ, ... ကဲ့သို့သော အင်္ဂလိပ် သို့မဟုတ် ဂရိအက္ခရာများကို အသုံးပြုသည်။ ဤစာလုံးများကို မသိသောပမာဏကို ကိုယ်စားပြုရန် အသုံးပြုပါသည်။ စာလုံးများသည် ဂဏန်းများကို ကိုယ်စားပြုသောကြောင့် ၎င်းတို့ကို ပကတိဂဏန်းများဟု ခေါ်သည်။ ပကတိနံပါတ်သည် မည်သည့်တန်ဖိုးကိုမဆို ယူဆနိုင်သောကြောင့် ၎င်းကို ကိန်းရှင် ဟုခေါ်သည်။ တိကျသောတန်ဖိုးရှိသော ဂဏန်းကို ကိန်း သေဟုခေါ်သည်။

အက္ခရာသင်္ချာအသုံးအနှုန်း

တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော ဂဏန်းသင်္ချာလုပ်ဆောင်ချက်များဖြင့် ချိတ်ဆက်ထားသော ကိန်းသေများနှင့် အက္ခရာများ(ကိန်းသေများ) ပေါင်းစပ်ခြင်းကို အက္ခရာသင်္ချာအညွှန်းကိန်းတစ်ခုဟုခေါ်သည်။ တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော လက္ခဏာများ (+, −) သည် အက္ခရာသင်္ချာအသုံးအနှုန်းကို အပိုင်းများစွာသို့ ပိုင်းခြားထားသည်။ ၎င်း၏သင်္ကေတပါရှိသောအစိတ်အပိုင်းတစ်ခုစီကို အက္ခရာသင်္ချာ အသုံးအနှုန်း တစ်ခုဟုခေါ်သည်။ ကိန်းသေတစ်ခုသည် ဥပမာ 4၊ ကိန်းသေတစ်ခု၊ ဥပမာ၊ x၊ ကိန်းသေနှင့်ကိန်းရှင်တစ်ခု၏ထုတ်ကုန်တစ်ခု၊ ဥပမာ၊ 4x သို့မဟုတ် ကိန်းရှင်နှစ်ခု သို့မဟုတ် ထို့ထက်ပိုသောကိန်းရှင်တစ်ခု၏ထုတ်ကုန်တစ်ခု၊ ဥပမာ၊ xy၊ xy ² ။

Monomial- ဝေါဟာရတစ်ခုတည်းသာရှိသော အက္ခရာသင်္ချာအသုံးအနှုန်းကို monomial ဟုခေါ်သည်။ ဥပမာ- 7x၊ ab ² ၊ 8
Binomial- ဝေါဟာရနှစ်ခုပါသော အက္ခရာသင်္ချာအသုံးအနှုန်းကို binomial ဟုခေါ်သည်။ ဥပမာ- x ² + y ² ၊ x + 2
Trinomial- ဝေါဟာရသုံးလုံးပါသော အက္ခရာသင်္ချာအသုံးအနှုန်းကို trinomial ဟုခေါ်သည်။ ဥပမာ- x ² + y ² + z ² , x + y +2

ကိန်းဂဏန်း

ထုတ်ကုန်တစ်ခုဖွဲ့စည်းရန် မြှောက်ထားသော ပမာဏတစ်ခုစီကို ကိန်းသေတစ်ခုဟုခေါ်ပြီး ထုတ်ကုန်တစ်ခုအတွင်းရှိ မည်သည့်အချက်ကိုမဆို ကျန်အချက်များ၏ ထုတ်ကုန်၏ ဖော်ကိန်းဟုခေါ်သည်။ အခေါ်အဝေါ်အရ -11p ² q ဟူသော စကားရပ်၏ 5p ³ − 11p ² q + 7၊

• ဂဏန်းကိန်းကိန်းသည် -11 ဖြစ်သည်။
• ပကတိကိန်းဂဏန်းသည် p ² q ဖြစ်သည်။
• p ² ၏ coefficient သည် -11q ဖြစ်သည်။
• -11p ² ၏ coefficient သည် q ဖြစ်သည်။
  

စည်းမျဥ်းများ နှင့် မတူပါ။

ကိန်းရှင်များ၏ တူညီသော ကိန်းရှင်(များ) နှင့် တူညီသော ထပ်ကိန်း(များ) ပါရှိသော အက္ခရာသင်္ချာအသုံးအနှုန်းများ ၏ စည်းကမ်းချက်များကို ဝေါဟာရများ နှင့်တူသည်ဟု ဆိုပါသည်။ အခေါ်အဝေါ်ကဲ့သို့ ကိန်းဂဏန်းများသာ ကွဲပြားနိုင်သည်။
2xy+ 3x + 4y + 5xy + 7y
2xy နှင့် 5xy ဝေါဟာရများသည် ဝေါဟာရများဖြစ်သည်။ 4y နှင့် 7y သည် ဝေါဟာရများနှင့်တူသည်။

အက္ခရာသင်္ချာအသုံးအနှုန်း 2x + 3xy + 5y ရှိ စည်းမျဥ်းများ အားလုံးနှင့် မတူပါ။

Polynomial

ပါဝင်သည့် ကိန်းရှင်များ၏ ပါဝါများသည် အနုတ်လက္ခဏာမဟုတ်သော ကိန်းပြည့်များဖြစ်သည့် အက္ခရာသင်္ချာအသုံးအနှုန်းကို ပေါင်းကူးအမည်ဟု ခေါ်သည်။

\(x^3+ x^2 + 2x + 1\) သည် ကိန်းရှင် x တစ်ခုတွင် ကိန်းဂဏန်းတစ်ခုဖြစ်သည်။
\(6x - \frac{4x}{y} + 2y + 3 \) အများကိန်းမဟုတ်ပါ (ဒုတိယအသုံးအနှုန်းတွင် y တွင် ပါဝါ-1 ရှိကြောင်း သတိပြုပါ)

Like စည်းမျဥ်းပေါင်းထည့်ခြင်းနှင့် နုတ်ခြင်း။

ပေါင်းစည်းခြင်း သို့မဟုတ် နုတ်ခြင်းဖြင့် ဝေါဟာရများကဲ့သို့ ပေါင်းစပ်ရန်အတွက် ပေးထားသော ကိန်းဂဏာန်းများ၏ ကိန်းဂဏန်းကိန်းကိန်းများကို ပေါင်းထည့်ခြင်း သို့မဟုတ် နုတ်ရုံသာဖြစ်သည်။
ဥပမာ-
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

အက္ခရာသင်္ချာအသုံးအနှုန်းများ၏ ပေါင်းထည့်ခြင်းနှင့် နုတ်ခြင်း။

အက္ခရာသင်္ချာအသုံးအနှုန်းကိုထည့်ရန်၊ ၎င်းတို့ကဲ့သို့ ဝေါဟာရများကို ရိုးရှင်းစွာထည့်ပါ။ အဆင်ပြေစေရန်အတွက် တူညီသောကော်လံတွင် အခြားတစ်ခု၏အောက်တွင် စာလုံးတစ်လုံးကို ရေးပါ။ ဥပမာ-
ထည့်ပါ -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

နုတ်ရန်အတွက် ၊ နုတ်နေသည့်အသုံးအနှုန်းတစ်ခုစီ၏ နိမိတ်ကိုလှန်ကာ ကိန်းဂဏန်းနှစ်ခုကို ပေါင်းထည့်ပါ။ ဥပမာ
\(3x^2 + 5x + 7y^2\) မှ \(9x^2 + 7x + 5y + 10y^2\) နုတ်ပါ။

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

အုပ်စုဖွဲ့ခြင်းကို အသုံးပြု၍ အက္ခရာသင်္ချာအသုံးအနှုန်းများကို ပေါင်းထည့်ခြင်း သို့မဟုတ် နုတ်ခြင်းတို့ ပြုလုပ်နိုင်သည်။ အပေါ်က ဥပမာကိုယူပြီး Grouping ကိုသုံးပြီး နုတ်ကြရအောင်။

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

အက္ခရာသင်္ချာအသုံးအနှုန်းများ မြှောက်ခြင်း။

အက္ခရာသင်္ချာအသုံးအနှုန်းကို မြှောက်၍ သုံးမျိုးခွဲခြားနိုင်သည်၊ ၎င်းတို့ကို သီးခြားဆွေးနွေးကြပါစို့။

ဖြစ်ရပ်မှန် ငါ (Multiplication of Monomials) : ၎င်းတို့၏ ကိန်းဂဏာန်းကိန်းများကို ပေါင်း၍ ဘုံကိန်းရှင်များ၏ ထပ်ကိန်းများကို ပေါင်းထည့်ခြင်းဖြင့်၊ ပုံမှန်မဟုတ်သော ကိန်းရှင်များကို မပြောင်းလဲပါ။ ဥပမာ- 6bc နှင့် 5b = ၏ ထုတ်ကုန်ကို ရှာပါ။ \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

ဖြစ်ရပ်မှန် II (Multiplication Polynomial by a Monomial) : အများကိန်း၏ သက်တမ်းတစ်ခုစီကို monomial ဖြင့် မြှောက်ပါ။ ဥပမာ- 3xy နှင့် x ² + 2xy + y ² ၏ ထုတ်ကုန်ဖြစ်သည်။
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

ဖြစ်ရပ်မှန် III (Polynomial of a Multiplication of a Polynomial by Polynomial) − ကိန်းဂဏန်းတစ်ခုစီ၏ ကိန်းဂဏန်းတစ်ခုစီကို အခြားဝေါဟာရတစ်ခုစီဖြင့် မြှောက်ပြီး ထုတ်ကုန်ကို ရိုးရှင်းစေရန် ထိုကဲ့သို့ ဝေါဟာရများကို ပေါင်းစပ်ပါ။ ဥပမာ- (2x + 3y) နှင့် ( x + y + 2) ၏ ထုတ်ကုန်
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

အက္ခရာသင်္ချာအသုံးအနှုန်းများ အပိုင်း

အက္ခရာသင်္ချာအသုံးအနှုန်းခွဲဝေခြင်းကို အောက်ပါကိစ္စရပ်သုံးခုဖြင့် ရှင်းပြနိုင်သည်။

ဖြစ်ရပ်မှန် ငါ (Monomial by a Monomial ဖြင့် ပိုင်းခြားခြင်း) − မိုနိုမီယာတစ်ခုအား monomial ဖြင့် ပိုင်းခြားရန်၊ ဘုံကိန်းရှင်များ၏ ထပ်ကိန်းများကို နုတ်ခြင်းဖြင့် ၎င်းတို့၏ ကိန်းဂဏာန်းကိန်းကိန်းများနှင့် ကိန်းရှင်များ၏ ကိုးအကန့်များကို ရှာပါ။
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

ဖြစ်ရပ်မှန် II (ပိုလီnomial ဖြင့် ခွဲဝေခြင်း) − အများကိန်း၏ သက်တမ်းတစ်ခုစီကို monomial ဖြင့် ပိုင်းပြီး အထက်ဖော်ပြပါ ကိစ္စရပ်တွင် ပေးထားသည့်အတိုင်း ပိုင်းခြားပါ။ ဥပမာ-
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

ဖြစ်ရပ်မှန် III ( Polynomial တစ်ခုဖြင့် ခွဲဝေခြင်း ) : ၎င်းကို ရှည်လျားသော ပိုင်းခြားမှုနည်းလမ်းဖြင့် လုပ်ဆောင်ပါမည်။ ဥပမာတစ်ခုသုံးပြီး ဒါကို နားလည်ဖို့ ကြိုးစားကြည့်ရအောင်။
\(8x^2 + 9x - 8 \div 8x + 1\)

quotient(x) ၏ပထမသက်တမ်းကိုရှာရန် ဂွင်(8x ² ) ၏ပထမသက်တမ်းကို ကိန်းကိန်း(8x) ဖြင့် ပိုင်းခြားခြင်းဖြင့် စတင်ပြီး ခွဲကိန်း(x) နှင့် ခွဲတမ်းကို မြှောက်ပြီး နုတ်ပါ။

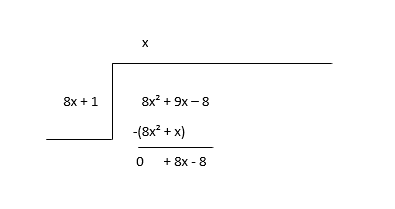
အကြွင်းကို ဂွင်အသစ်အဖြစ် ထည့်သွင်းစဉ်းစားပြီး လဒ်၏ နောက်သက်တမ်းကို ခန့်မှန်းပါ။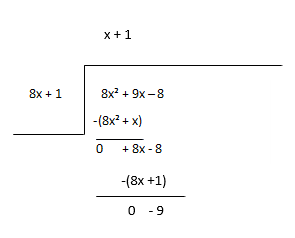

Quotient - x + 1၊ Remainder - -9

ကွင်းစကွင်းပိတ်များကို ဖယ်ရှားခြင်းနှင့် လည်ပတ်မှုစည်းမျဉ်း၏ အမိန့်ကို အသုံးပြုခြင်း။

ကွင်းစကွင်းပိတ်များပါရှိသော အက္ခရာသင်္ချာအသုံးအနှုန်းကို ရိုးရှင်းစေရန်၊ အစီအစဥ်အတိုင်း ကွင်းပိတ်များကို ဖယ်ရှားပါ-

ဥပမာ-
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)