Back to the topics list

बीजगणित अभिव्यक्ति

सामग्री:

• एक चर के हो?
• बीजगणितीय अभिव्यक्तिका प्रकारहरू।
• गुणांक।
• लाइक र अनलाइक सर्तहरू।
• बहुपद।
• बीजगणितीय अभिव्यक्तिको जोड, घटाउ, गुणन र भाग।
• बीजगणितीय अभिव्यक्ति सरल बनाउन को लागी सञ्चालन नियम को आदेश को आवेदन।

शाब्दिक संख्याहरू

बीजगणितमा हामी संख्याहरू प्रतिनिधित्व गर्न अङ्ग्रेजी वा ग्रीक अक्षरहरू जस्तै a, b, x, y, β, Φ, ... प्रयोग गर्छौं। यी अक्षरहरू अज्ञात मात्राहरू प्रतिनिधित्व गर्न प्रयोग गरिन्छ। अक्षरहरूले संख्याहरू प्रतिनिधित्व गर्ने हुनाले तिनीहरूलाई शाब्दिक संख्याहरू भनिन्छ। शाब्दिक संख्याले कुनै पनि मान मान्न सक्छ त्यसैले हामी यसलाई चर भन्छौं। निश्चित मान भएको संख्यालाई स्थिरता भनिन्छ।

बीजगणितीय अभिव्यक्ति

एक वा धेरै अंकगणितीय कार्यहरू (जोड, गुणन, घटाउ, भाग) द्वारा जोडिएको स्थिरांक र अक्षरहरू (चर) को संयोजनलाई बीजगणितीय अभिव्यक्ति भनिन्छ। एक वा बढी चिन्हहरू (+, -) बीजगणितीय अभिव्यक्तिलाई धेरै भागहरूमा विभाजन गर्दछ। यसको चिन्ह सहितको प्रत्येक भागलाई बीजगणितीय अभिव्यक्तिको शब्द भनिन्छ। एक शब्द एक स्थिर जस्तै हुन सक्छ उदाहरण को लागी 4, एक चर, उदाहरण को लागी, x, एक स्थिर र चर को उत्पादन, उदाहरण को लागी, 4x वा दुई वा बढी चर को उत्पादन, उदाहरण को लागी, xy, xy ² ।

मोनोमियल: एक मात्र पद भएको बीजगणितीय अभिव्यक्तिलाई मोनोमियल भनिन्छ। उदाहरण: 7x, ab ² , 8
द्विपद: दुई पदहरू भएको बीजगणितीय अभिव्यक्तिलाई द्विपद भनिन्छ। उदाहरण: x ² + y ² , x + 2
त्रिनोमियल: तीन पदहरू भएको बीजगणितीय अभिव्यक्तिलाई त्रिनोमियल भनिन्छ। उदाहरण: x ² + y ² + z ² , x +y +2

गुणांक

प्रत्येक परिमाण (स्थिर वा शाब्दिक) गुणन गरी गुणनफल बनाइन्छ, त्यसलाई गुणनफलको कारक भनिन्छ र उत्पादनको कुनै पनि कारकलाई बाँकी कारकहरूको गुणनफल भनिन्छ। शब्दमा, -11p ² q अभिव्यक्तिको 5p ³ − 11p ² q + 7,

• संख्यात्मक गुणांक -11 हो।
• शाब्दिक गुणांक p ² q हो।
• p ² को गुणांक -11q हो।
• -11p ² को गुणांक q हो।
  

लाइक र अनलाइक सर्तहरू

एउटै चर (हरू) र चरहरूको एउटै घातांक (हरू) भएको बीजगणितीय अभिव्यक्तिका सर्तहरूलाई पदहरू जस्तै भनिन्छ। जस्तै शब्द गुणांकमा मात्र फरक हुन सक्छ।
2xy + 3x + 4y + 5xy + 7y
सर्तहरू 2xy र 5xy शब्दहरू जस्तै छन्। 4y र 7y शब्दहरू जस्तै छन्।

बीजगणितीय अभिव्यक्ति 2x + 3xy + 5y मा सर्तहरू सबै विपरीत छन्।

बहुपद

एक बीजगणितीय अभिव्यक्ति जसमा चरहरूको शक्तिहरू गैर-ऋणात्मक पूर्णांकहरू हुन्, बहुपद भनिन्छ।

\(x^3+ x^2 + 2x + 1\) एउटा चर x मा बहुपद हो।
\(6x - \frac{4x}{y} + 2y + 3 \) बहुपद होइन (ध्यान दिनुहोस् कि दोस्रो पदमा y को शक्ति -1 छ)

लाइक सर्तहरूको जोड र घटाउ

थप वा घटाउ द्वारा जस्तै सर्तहरू संयोजन गर्न, दिइएको सर्तहरूको संख्यात्मक गुणांकहरू जोड्नुहोस् वा घटाउनुहोस्।
उदाहरण:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

बीजगणितीय अभिव्यक्तिको जोड र घटाउ

बीजगणितीय अभिव्यक्ति थप्नको लागि, तिनीहरूको जस्तै पदहरू थप्नुहोस्। सुविधाको लागि एउटै स्तम्भमा अर्को तल एक जस्तै शब्द लेख्नुहोस्। उदाहरण:
थप्नुहोस् -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

घटाउको लागि, घटाइएको अभिव्यक्तिको प्रत्येक पदको चिन्हलाई फ्लिप गर्नुहोस् र त्यसपछि दुई अभिव्यक्तिलाई सँगै जोड्नुहोस्। उदाहरण
\(9x^2 + 7x \(9x^2 + 7x + 5y + 10y^2\) \(3x^2 + 5x + 7y^2\) बाट \(3x^2 + 5x + 7y^2\) घटाउनुहोस्

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

तपाईं समूहीकरण प्रयोग गरेर बीजगणितीय अभिव्यक्तिहरू थप्न वा घटाउन सक्नुहुन्छ। माथिको उदाहरण लिनुहोस् र समूहीकरण प्रयोग गरेर घटाउनुहोस्:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

बीजगणितीय अभिव्यक्तिको गुणन

बीजगणितीय अभिव्यक्तिको गुणनलाई तीन अवस्थामा विभाजन गर्न सकिन्छ, तिनीहरूलाई छुट्टै छलफल गरौं:

केस म (Multplication of Monomials) : तिनीहरूको संख्यात्मक गुणांकलाई सँगै गुणन गर्नुहोस् र त्यसपछि सामान्य चरहरूको घातांकहरू जोडेर, असामान्य चरहरूलाई अपरिवर्तित छोड्नुहोस्। उदाहरण: 6bc र 5b = को गुणन पत्ता लगाउनुहोस् \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

केस II (एकपदद्वारा गुणन बहुपद) : बहुपदको प्रत्येक पदलाई मोनोमियलद्वारा गुणन गर्नुहोस्। उदाहरण: 3xy र x ² + 2xy + y ² को गुणन हो
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

केस III (बहुपदद्वारा बहुपदको गुणन) : एउटा बहुपदको प्रत्येक पदलाई अर्कोको प्रत्येक पदले गुणन गर्नुहोस् र त्यसपछि समान पदहरूलाई मिलाएर गुणनलाई सरल बनाउनुहोस्। उदाहरण: (2x + 3y) र (x + y + 2) को उत्पादन हो
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

बीजगणितीय अभिव्यक्ति को विभाजन

बीजगणितीय अभिव्यक्तिको विभाजनलाई तलका तीनवटा केसहरू प्रयोग गरेर व्याख्या गर्न सकिन्छ।

केस म (मोनोमियलद्वारा मोनोमियलको विभाजन) : मोनोमियललाई मोनोमियलले विभाजन गर्न, सामान्य चरहरूको घातांक घटाएर तिनीहरूको संख्यात्मक गुणांक र चरहरूको भागफल पत्ता लगाउनुहोस्। उदाहरण:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

केस II (एकपदीद्वारा बहुपदको विभाजन) : बहुपदको प्रत्येक पदलाई मोनोमियलले विभाजन गर्नुहोस् र त्यसपछि माथिको अवस्थामा दिइए अनुसार विभाजन गर्नुहोस्। उदाहरण:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

केस III ( एक बहुपद द्वारा एक बहुपद को विभाजन ): यो लामो विभाजन विधि द्वारा गरिनेछ। यसलाई एउटा उदाहरण प्रयोग गरेर बुझ्ने प्रयास गरौं।
\(8x^2 + 9x - 8 \div 8x + 1\)

भागफल(x) को पहिलो पद पत्ता लगाउन भाजकको पहिलो पद (8x) सँग लाभांशको पहिलो पद (8x ² ) भाग गरेर सुरु गर्नुहोस् र त्यसपछि तपाईंले भागफल पदलाई भाजकसँग गुणन गर्नुहोस् र घटाउनुहोस्।

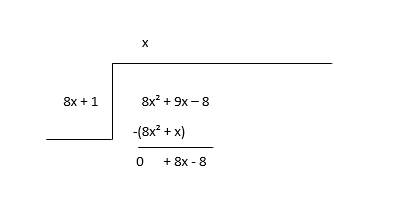
बाँकीलाई नयाँ लाभांशको रूपमा विचार गर्नुहोस् र भागफलको अर्को अवधि अनुमान गर्नुहोस्।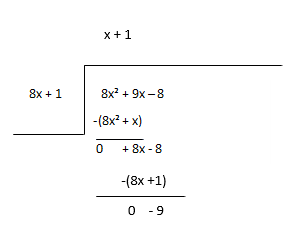

भागफल - x + 1, शेष - -9

कोष्ठक हटाउने र सञ्चालन नियमको आदेशको प्रयोग

कोष्ठकहरू भएको बीजगणितीय अभिव्यक्तिलाई सरल बनाउन कोष्ठकहरूलाई निम्न क्रममा हटाउनुहोस्:

उदाहरण:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)