Back to the topics list

algebraïsche uitdrukking

Inhoud:

• Wat is een variabele?
• Soorten algebraïsche uitdrukkingen.
• Coëfficiënt.
• Vind ik leuk en niet leuk.
• Polynoom.
• Optellen, aftrekken, vermenigvuldigen en delen van algebraïsche uitdrukkingen.
• Toepassing van de regel van de volgorde van bewerkingen om de algebraïsche uitdrukking te vereenvoudigen.

Letterlijke cijfers

In Algebra gebruiken we Engelse of Griekse alfabetten zoals a, b, x, y, β, Φ, ... om getallen weer te geven. Deze letters worden gebruikt om onbekende hoeveelheden weer te geven. Aangezien letters getallen vertegenwoordigen, worden ze letterlijke getallen genoemd. Een letterlijk getal kan elke waarde aannemen, daarom noemen we het een variabele . Een getal met een bepaalde waarde wordt een constante genoemd.

Algebraïsche uitdrukking

Een combinatie van constanten en letterlijke getallen (variabelen) verbonden door een of meer rekenkundige bewerkingen (optellen, vermenigvuldigen, aftrekken, delen) wordt een algebraïsche uitdrukking genoemd. Een of meer tekens (+, −) breken een algebraïsche uitdrukking in verschillende delen. Elk deel met zijn teken wordt een term van de algebraïsche uitdrukking genoemd. Een term kan een constante zijn zoals bijvoorbeeld 4, een variabele, bijvoorbeeld x, een product van een constante en variabele, bijvoorbeeld 4x of een product van twee of meer variabelen, bijvoorbeeld xy, xy ² .

Monomial: Een algebraïsche uitdrukking die slechts één term heeft, wordt een monomial genoemd. Voorbeeld: 7x, ab ² , 8
Binomiaal: Een algebraïsche uitdrukking die twee termen heeft, wordt een binominale uitdrukking genoemd. Voorbeeld: x ² + y ² , x + 2
Trinominaal: Een algebraïsche uitdrukking die drie termen heeft, wordt een trinominaal genoemd. Voorbeeld: x ² + y ² + z ² , x +y +2

Coëfficiënt

Elk van de hoeveelheden (constante of letterlijke getallen) vermenigvuldigd om een product te vormen, wordt een factor van het product genoemd en elke factor in een product wordt de coëfficiënt van het product van de resterende factoren genoemd. In de term, -11p ² q van de uitdrukking 5p ³ − 11p ² q + 7,

• De numerieke coëfficiënt is -11.
• Letterlijke coëfficiënt is p ² q.
• Coëfficiënt van p ² is -11q.
• Coëfficiënt van -11p ² is q.
  

Vind ik leuk en niet leuk

De termen van de algebraïsche uitdrukking met dezelfde variabele(n) en dezelfde exponent(en) van de variabelen worden gelijksoortige termen genoemd. Dezelfde term kan alleen verschillen in coëfficiënten.
2xy+ 3x + 4j + 5xy + 7j
De termen 2xy en 5xy lijken op termen. 4y en 7y zijn als termen.

Termen in de algebraïsche uitdrukking 2x + 3xy + 5y zijn allemaal verschillend.

Polynoom

Een algebraïsche uitdrukking waarin de machten van de betrokken variabelen niet-negatieve gehele getallen zijn, wordt een polynoom genoemd.

\(x^3+ x^2 + 2x + 1\) is een polynoom in één variabele x.
\(6x - \frac{4x}{y} + 2y + 3 \) is geen polynoom (merk op dat y in de tweede term de macht -1 heeft)

Optellen en aftrekken van soortgelijke termen

Om gelijke termen te combineren door optellen of aftrekken, hoeft u alleen maar de numerieke coëfficiënten van de gegeven termen op te tellen of af te trekken.
Voorbeeld:
\(3x + 4x = (3+4) x = 7x \\ 7x - 5x = (7-5)x = 2x\)

Optellen en aftrekken van algebraïsche uitdrukkingen

Om algebraïsche uitdrukkingen toe te voegen, voegt u eenvoudig hun termen toe. Schrijf voor het gemak de soortgelijke term onder elkaar in dezelfde kolom. Voorbeeld:
Toevoegen -
\(3x^2 + 5x + 9xy + \;2y + 7y^2\) , \(2x + 4xy + y\) , \(x^2\; + 2x + 3xy + 6y + 3y^2\)

\(\;\;\;\;\;3x^2 + 5x + 9xy + \;2y + 7y^2 \\ \;\;\;\;\;\;\;0\;\;+ 2x + 4xy + \;\;y+ 0 \\ + \;\;\;\underline{x^2\; + 2x + 3xy + 6y + 3y^2} \\ \;\;\;\;4x^2 \;\;+ 9x +16xy+ 9y + 10y^2 \)

Draai voor aftrekken het teken van elke term van de uitdrukking die wordt afgetrokken om en tel vervolgens de twee uitdrukkingen bij elkaar op. Voorbeeld
Trek \(3x^2 + 5x + 7y^2\) af van \(9x^2 + 7x + 5y + 10y^2\)

\(\;\;\;\;\;9x^2 + 7x + 5y + 10y^2 \\ \;\;\underline{-3x^2 - 5x \;\;\;\;\;\;\; \;- \;7y^2} \\ \;\;\;\;6x^2 \;\;+ 2x + 5y + 3y^2 \)

U kunt ook algebraïsche uitdrukkingen optellen of aftrekken met behulp van Groeperen. Laten we het bovenstaande voorbeeld nemen en aftrekken met Groeperen:

\((9-3)x^2 + (7-5) x + 5y + (10 - 7)y^2 = 6x^2 + 2x + 5y + 3y^2\)

Vermenigvuldiging van algebraïsche uitdrukkingen

Vermenigvuldiging van algebraïsche expressie kan worden onderverdeeld in drie gevallen, laten we ze afzonderlijk bespreken:

Geval l (Vermenigvuldiging van monomials) : Vermenigvuldig hun numerieke coëfficiënten met elkaar en vervolgens de variabelen door de exponenten van gemeenschappelijke variabelen toe te voegen, waarbij de ongebruikelijke variabelen ongewijzigd blijven. Voorbeeld: Zoek het product van 6bc en 5b = \( (6 × 5) (c)(b^{1+1}) = 30 cb^2\)

Geval II (Vermenigvuldiging polynoom met een monomiaal) : Vermenigvuldig elke term van de polynoom met de monomiaal. Voorbeeld: Product van 3xy en x ² + 2xy + y ² is
\(3xy(x^2+ 2xy + y^2) = (3xy ⋅ x^2) + (3xy ⋅ 2xy) + (3xy ⋅ y^2) = 3x^3y + 6x^2y^2+3xy^3\)

Geval III (Vermenigvuldiging van een polynoom met polynoom) : Vermenigvuldig elke term van de ene polynoom met elke term van de andere en combineer vervolgens soortgelijke termen om het product te vereenvoudigen. Voorbeeld: Product van (2x + 3y) en ( x + y + 2) is
\((2x + 3y) ⋅ (x + y + 2) = 2x( x + y + 2) + 3y(x + y + 2) \\ 2x^2 + 2xy + 4x + 3yx + 3y^2 + 6y\\ 2x^2 + 5xy + 4x + 3y^2 + 6y\)

Verdeling van algebraïsche uitdrukkingen

De verdeling van algebraïsche expressie kan worden uitgelegd aan de hand van onderstaande drie gevallen.

Geval l (Deling van een monomiaal door een monomiaal) : Om een monomiaal door een monomiaal te delen, zoekt u de quotiënten van hun numerieke coëfficiënten en de quotiënten van de variabelen door de exponenten van gemeenschappelijke variabelen af te trekken. Voorbeeld:
\(18m^6x ÷ 2m^4x^2 = \frac{18m^6x}{2m^4x^2} = \frac{9m^2}{x}\)

Geval II (Deling van polynoom door monomiaal) : deel elke term van het polynoom door een monomiaal en deel vervolgens zoals gegeven in het bovenstaande geval. Voorbeeld:
\((20x^2 + 40xy + 25y^2) \div 5xy \)
\(= \frac{20x^2}{5xy} + \frac{40xy}{5xy} + \frac{25y^2}{5xy}\)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)
\(= \frac{4x}{y} + 8 + \frac{5y}{x} \)

Geval III ( Deling van een polynoom door een polynoom ): Dit wordt gedaan volgens de staartdelingsmethode. Laten we dit proberen te begrijpen aan de hand van een voorbeeld.
\(8x^2 + 9x - 8 \div 8x + 1\)

Begin met het delen van de eerste term van het deeltal(8x ² ) met de eerste term van de deler(8x) om de eerste term van het quotiënt(x) te vinden en dan vermenigvuldig je de quotiëntterm met de deler en trek je af.

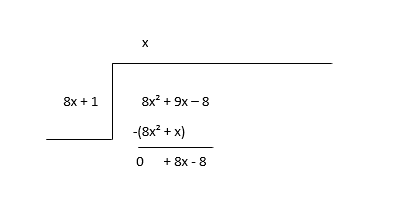
Beschouw de rest als het nieuwe deeltal en schat de volgende term van het quotiënt.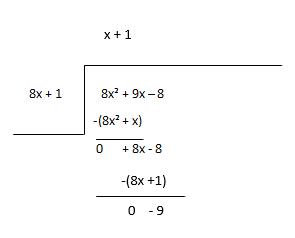

Quotiënt - x + 1, Rest - -9

Verwijdering van haakjes en gebruik van de regel van de volgorde van bewerkingen

Om een algebraïsche uitdrukking met haakjes te vereenvoudigen, verwijdert u de haakjes in de volgende volgorde:

Voorbeeld:
\(7 - [ x -{2y - (6x + y + 7)} + 3x ] \\ 7 - [ x - {2y - 6x - y - 7} + 3x] \\ 7 - [-2x - 3y - 7] \\ 7 +2x + 3y + 7 \\ 2x +3 y+ 14 \\\)